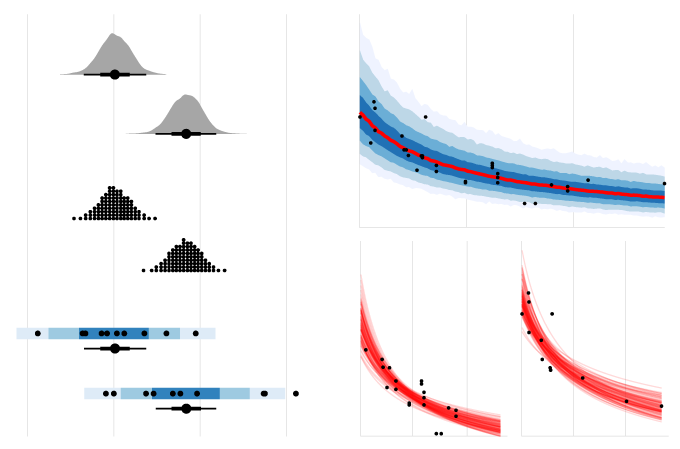
tidybayes: Bayesian analysis + tidy data + geoms

tidybayes is an R package that aims to make it easy to integrate popular Bayesian modelling methods into a tidy data + ggplot workflow.

Tidy data frames (one observation per row) are particularly convenient for use in a variety of R data manipulation and visualization packages. However, when using MCMC / Bayesian samplers like JAGS or Stan in R, we often have to translate this data into a form the sampler understands, and then after running the model, translate the resulting sample (or predictions) into a more tidy format for use with other R functions. tidybayes aims to simplify these two common (often tedious) operations:

• Composing data for use with the sampler. This often means translating data from a data.frame into a list , making sure factors are encoded as numerical data, adding variables to store the length of indices, etc. This package helps automate these operations using the compose_data function, which automatically handles data types like numeric, logical, factor, and ordinal, and allows easy extensions for converting other datatypes into a format the sampler understands by providing your own implementation of the generic as_data_list.

• Extracting tidy samples from the sampler. This often means extracting indices from parameters with names like "b[1,1]", "b[1,2]" into separate columns of a data frame, like i = c(1,1,..) and j = c(1,2,...). More tediously, sometimes these indices actually correspond to levels of a factor in the original data; e.g. "x[1]" might correspond to a value of x for the first level of some factor. We provide several straightforward ways to convert samples of a variable with indices into useful long-format ("tidy") data frames, with automatic back-conversion of common data types (factors, logicals) using the spread_samples and gather_sampels functions, including automatic recovery of factor levels corresponding to variable indices. In most cases this kind of long-format data is much easier to use with other data-manipulation and plotting packages (e.g., dplyr, tidyr, ggplot2) than the format provided by default from the sampler.

tidybayes also provides some additional functionality for data manipulation and visualization tasks common to many models:

• Extracting tidy fits and predictions from models. For models like those provided by rstanarm and brms, tidybayes provides a tidy analog of the fitted and predict functions, called add_fitted_samples and add_predicted_samples. These functions are modeled after the modelr::add_predictions function, and turn a grid of predictions into a long-format data frame of samples from either the fits or predictions from a model. These functions make it straightforward to generate arbitrary fit lines from a model.

• Summarizing posterior distributions from models. The point_interval family of functions (mean_qi, median_qi, mode_hdi, etc) are methods for generating estimates and intervals that are designed with tidy workflows in mind. They can generate estimates plus an arbitrary number of probability intervals from tidy data frames of samples, they return tidy data frames, and they respect data frame groups.

• Visualizing posteriors. The focus on tidy data makes the output from tidybayes easy to visualize using ggplot. Existing geoms (like geom_pointrange and geom_linerange) can give useful output, but tidybayes also includes several geoms to simplify common combinations of stats and geoms with sensible defaults suitable for visualizing posterior estimates and intervals (geom_pointinterval, geom_pointintervalh, stat_pointinterval, stat_pointintervalh), visualizing densities with point estimates and intervals ("eye plots", geom_eye and geom_eyeh; or "half-eye plots", geom_halfeyeh), and visualizing fit lines with an arbitrary number of uncertainty bands (geom_lineribbon and stat_lineribbon). Combining the base-R quantile function with geom_dotplot also facilitates the contruction of quantile dotplots of posteriors (see example in this document).

• Comparing a variable across levels of a factor, which often means first generating pairs of levels of a factor (according to some desired set of comparisons) and then computing a function over the value of the comparison variable for those pairs of levels. Assuming your data is in the format returned by spread_samples, the compare_levels function allows comparison across levels to be made easily.

Finally, tidybayes aims to fit into common workflows through compatibility with other packages:

• Compatibility with other tidy packages. Default column names in the output have also been chosen for compatibility with broom::tidy, which makes comparison with estimates from non-Bayesian models straightforward.

• Compatibility with non-tidy packages. The unspread_samples and ungather_samples functions invert spread_samples and gather_samples, aiding compatiblity with other Bayesian plotting packages (notably bayesplot). The gather_emmeans_samples function turns the output from emmeans::emmeans (formerly lsmeans) into long-format data frames (when applied to supported model types, like MCMCglmm and rstanarm models).

Supported model types

tidybayes aims to support a variety of models with a uniform interface. Currently supported models include rstan, coda::mcmc and coda::mcmc.list, runjags, rstanarm, brms, MCMCglmm, and anything with its own as.mcmc.list implementation. If you install the tidybayes.rethinking package, models from the rethinking package are also supported.

Installation

tidybayes is not yet on CRAN, but I am in the process of preparing a CRAN submission. You can track progress towards the CRAN submission at the CRAN Milestone.

In the mean time, you can install the latest development version from GitHub with these R commands:

install.packages("devtools")
devtools::install_github("mjskay/tidybayes")

Examples

This example shows the use of tidybayes with the Stan modeling language; however, tidybayes supports many other samplers and models, such as JAGS, brm, rstanarm, and (theoretically) any model type supported by coda::as.mcmc.list.

library(magrittr)
library(dplyr)
library(ggplot2)
library(ggstance)
library(rstan)
library(tidybayes)
library(emmeans)
library(broom)
library(brms)
library(modelr)
library(forcats)
library(dotwhisker)

Imagine this dataset:

set.seed(5)
n = 10
n_condition = 5
ABC =
  data_frame(
    condition = rep(c("A","B","C","D","E"), n),
    response = rnorm(n * 5, c(0,1,2,1,-1), 0.5)
  )

ABC %>%
  ggplot(aes(x = response, y = condition)) +
  geom_point(alpha = 0.5) +
  ylab("condition")

A hierarchical model of this data might estimate an overall mean across the conditions (overall_mean), the standard deviation of the condition means (condition_mean_sd), the mean within each condition (condition_mean[condition]) and the standard deviation of the responses given a condition mean (response_sd):

data {
  int<lower=1> n;
  int<lower=1> n_condition;
  int<lower=1, upper=n_condition> condition[n];
  real response[n];
}
parameters {
  real overall_mean;
  vector[n_condition] condition_zoffset;
  real<lower=0> response_sd;
  real<lower=0> condition_mean_sd;
}
transformed parameters {
  vector[n_condition] condition_mean;
  condition_mean = overall_mean + condition_zoffset * condition_mean_sd;
}
model {
  response_sd ~ cauchy(0, 1);         // => half-cauchy(0, 1)
  condition_mean_sd ~ cauchy(0, 1);   // => half-cauchy(0, 1)
  overall_mean ~ normal(0, 5);
  condition_zoffset ~ normal(0, 1);   // => condition_mean ~ normal(overall_mean, condition_mean_sd)
  for (i in 1:n) {
    response[i] ~ normal(condition_mean[condition[i]], response_sd);
  }
}

## In file included from /home/jose/R/x86_64-pc-linux-gnu-library/3.4/BH/include/boost/config.hpp:39:0,
##                  from /home/jose/R/x86_64-pc-linux-gnu-library/3.4/BH/include/boost/math/tools/config.hpp:13,
##                  from /home/jose/R/x86_64-pc-linux-gnu-library/3.4/StanHeaders/include/stan/math/rev/core/var.hpp:7,
##                  from /home/jose/R/x86_64-pc-linux-gnu-library/3.4/StanHeaders/include/stan/math/rev/core/gevv_vvv_vari.hpp:5,
##                  from /home/jose/R/x86_64-pc-linux-gnu-library/3.4/StanHeaders/include/stan/math/rev/core.hpp:12,
##                  from /home/jose/R/x86_64-pc-linux-gnu-library/3.4/StanHeaders/include/stan/math/rev/mat.hpp:4,
##                  from /home/jose/R/x86_64-pc-linux-gnu-library/3.4/StanHeaders/include/stan/math.hpp:4,
##                  from /home/jose/R/x86_64-pc-linux-gnu-library/3.4/StanHeaders/include/src/stan/model/model_header.hpp:4,
##                  from filed346ca217a1.cpp:8:
## /home/jose/R/x86_64-pc-linux-gnu-library/3.4/BH/include/boost/config/compiler/gcc.hpp:186:0: warning: "BOOST_NO_CXX11_RVALUE_REFERENCES" redefined
##  #  define BOOST_NO_CXX11_RVALUE_REFERENCES
##  ^
## <command-line>:0:0: note: this is the location of the previous definition

Composing data for input to model: compose_data

We have compiled and loaded this model into the variable ABC_stan. Rather than munge the data into a format Stan likes ourselves, we will use the tidybayes::compose_data function, which takes our ABC data frame and automatically generates a list of the following elements:

• n: number of observations in the data frame
• n_condition: number of levels of the condition factor
• condition: a vector of integers indicating the condition of each observation
• response: a vector of observations

So we can skip right to modeling:

m = sampling(ABC_stan, data = compose_data(ABC), control = list(adapt_delta=0.99))

Getting tidy samples from the model: spread_samples

We decorate the fitted model using tidybayes::recover_types, which will ensure that numeric indices (like condition) are back-translated back into factors when we extract data:

m %<>% recover_types(ABC)

Now we can extract parameters of interest using spread_samples, which automatically parses indices, converts them back into their original format, and turns them into data frame columns. This function accepts a symbolic specification of Stan variables using the same syntax you would to index columns in Stan. For example, we can extract the condition means and the residual standard deviation:

m %>%
  spread_samples(condition_mean[condition], response_sd) %>%
  head(15)  # just show the first few rows

.chain	.iteration	condition	condition_mean	response_sd
1	1	A	-0.0488381	0.5824056
1	1	B	1.1920197	0.5824056
1	1	C	1.8984306	0.5824056
1	1	D	0.9617923	0.5824056
1	1	E	-0.8784776	0.5824056
1	2	A	0.1930336	0.5961389
1	2	B	1.0703175	0.5961389
1	2	C	1.9749954	0.5961389
1	2	D	1.1242398	0.5961389
1	2	E	-1.0909016	0.5961389
1	3	A	0.2633968	0.5559389
1	3	B	0.7562821	0.5559389
1	3	C	1.5831328	0.5559389
1	3	D	1.1647897	0.5559389
1	3	E	-0.8511654	0.5559389

The condition numbers are automatically turned back into text ("A", "B", "C", ...) and split into their own column. A long-format data frame is returned with a row for every iteration × every combination of indices across all variables given to spread_samples; for example, because response_sd here is not indexed by condition, within the same iteration it has the same value for each row corresponding to a different condition (some other formats supported by tidybayes are discussed in vignette("tidybayes"); in particular, the format returned by gather_samples).

Plotting posteriors as eye plots: geom_eye / geom_eyeh

Automatic splitting of indices into columns makes it easy to plot the condition means here. We will employ the tidybayes::geom_eyeh geom (horizontal version of tidybayes::geom_eye), which combines a violin plot of the posterior density, mean, and 95% quantile interval to give an "eye plot" of the posterior. The point and interval types are customizable using the point_interval family of functions. A "half-eye" plot (non-mirrored density) is also available as tidybayes::geom_halfeyeh.

m %>%
  spread_samples(condition_mean[condition]) %>%
  ggplot(aes(x = condition_mean, y = condition)) +
  geom_eyeh()

Or one can employ the similar "half-eye" plot:

m %>%
  spread_samples(condition_mean[condition]) %>%
  ggplot(aes(x = condition_mean, y = condition)) +
  geom_halfeyeh()

Plotting posteriors as quantile dotplots

Intervals are nice if the alpha level happens to line up with whatever decision you are trying to make, but getting a shape of the posterior is better (hence eye plots, above). On the other hand, making inferences from density plots is imprecise (estimating the area of one shape as a proportion of another is a hard perceptual task). Reasoning about probability in frequency formats is easier, motivating quantile dotplots, which also allow precise estimation of arbitrary intervals (down to the dot resolution of the plot, here 100):

m %>%
  spread_samples(condition_mean[condition]) %>%
  do(data_frame(condition_mean = quantile(.$condition_mean, ppoints(100)))) %>%
  ggplot(aes(x = condition_mean)) +
  geom_dotplot(binwidth = .04) +
  facet_grid(fct_rev(condition) ~ .) +
  scale_y_continuous(breaks = NULL)

The idea is to get away from thinking about the posterior as indicating one canonical point or interval, but instead to represent it as (say) 100 approximately equally likely points.

Model comparison via compatibility with broom

The output of the tidybayes::mean_qi function (and other point_interval functions) is compatible with broom::tidy, so we can compare parameter estimates easily to models supported by broom.

For example, let's compare to ordinary least squares (OLS) regression:

linear_estimates = 
  lm(response ~ condition, data = ABC) %>% 
  emmeans(~ condition) %>% 
  tidy() %>%
  mutate(model = "OLS")
linear_estimates

condition	estimate	std.error	df	conf.low	conf.high	model
A	0.1815842	0.173236	45	-0.1673310	0.5304993	OLS
B	1.0142144	0.173236	45	0.6652993	1.3631296	OLS
C	1.8745839	0.173236	45	1.5256687	2.2234990	OLS
D	1.0271794	0.173236	45	0.6782642	1.3760946	OLS
E	-0.9352260	0.173236	45	-1.2841411	-0.5863108	OLS

The output from mean_qi when given a single parameter uses conf.low and conf.high for interval names so that it lines up with tidy:

bayes_estimates = m %>%
  spread_samples(condition_mean[condition]) %>%
  mean_qi(estimate = condition_mean) %>%
  mutate(model = "Bayes")
bayes_estimates

condition	estimate	conf.low	conf.high	.prob	model
A	0.1932541	-0.1374798	0.5480979	0.95	Bayes
B	1.0054696	0.6559603	1.3464413	0.95	Bayes
C	1.8387243	1.4854153	2.1840288	0.95	Bayes
D	1.0128393	0.6541362	1.3738020	0.95	Bayes
E	-0.8927953	-1.2404690	-0.5443226	0.95	Bayes

This makes it easy to bind the two estimates together and plot them:

bind_rows(linear_estimates, bayes_estimates) %>%
  ggplot(aes(y = condition, x = estimate, xmin = conf.low, xmax = conf.high, color = model)) +
  geom_pointrangeh(position = position_dodgev(height = .3))

Shrinkage towards the overall mean is visible in the Bayesian estimates.

Comptability with broom::tidy also gives compatibility with dotwhisker::dwplot:

bind_rows(linear_estimates, bayes_estimates) %>%
  rename(term = condition) %>%
  dotwhisker::dwplot()

Posterior prediction and complex custom plots

The tidy data format returned by spread_samples also facilitates additional computation on parameters followed by the construction of more complex custom plots. For example, we can generate posterior predictions easily, and use the .prob argument (passed intervally to mean_qi) to generate any number of intervals from the posterior predictions, then plot them alongside parameter estimates and the data:

m %>%
  spread_samples(condition_mean[condition], response_sd) %>%
  mutate(pred = rnorm(n(), condition_mean, response_sd)) %>%
  ggplot(aes(y = condition)) +
  
  # posterior predictive intervals
  stat_intervalh(aes(x = pred), .prob = c(.5, .8, .95)) +
  scale_color_brewer() +
  
  # mean and quantile intervals of condition mean
  stat_pointintervalh(aes(x = condition_mean), .prob = c(.66, .95), position = position_nudge(y = -0.2)) +
  
  # data
  geom_point(data = ABC, aes(x = response, y = condition), inherit.aes = FALSE)

This plot shows 66% and 95% quantile credible intervals of posterior mean for each condition (point + black line); 95%, 80%, and 50% posterior predictive intervals (blue); and the data.

Fit curves

For models that support it (like rstanarm and brms models), We can also use the add_fitted_samples or add_predicted_samples functions to generate posterior fits or predictions. Combined with the functions from the modelr package, this makes it easy to generate fit curves.

Let's fit a slightly naive model to miles per gallon versus horsepower in the mtcars dataset:

m_mpg = brm(mpg ~ log(hp), data = mtcars, family = lognormal)

Now we will use modelr::data_grid, tidybayes::add_predicted_samples, and tidybayes::stat_lineribbon to generate a fit curve with multiple probability bands:

mtcars %>%
  data_grid(hp = seq_range(hp, n = 101)) %>%
  add_predicted_samples(m_mpg) %>%
  ggplot(aes(x = hp)) +
  stat_lineribbon(aes(x = hp, y = pred), .prob = c(.99, .95, .8, .5), inherit.aes = FALSE) +
  geom_point(aes(y = mpg, x = hp), data = mtcars, inherit.aes = FALSE) +
  scale_fill_brewer()

stat_lineribbon(aes(y = pred), .prob = c(.99, .95, .8, .5)) is one of several shortcut geoms that simplify common combinations of tidybayes functions and ggplot goems. It is roughly equivalent to the following:

  stat_summary(
    aes(y = pred, fill = forcats::fct_rev(ordered(...prob..)), group = -...prob..), 
    geom = "ribbon", fun.data = median_qi, fun.args = list(.prob = c(.99, .95, .8, .5))
  ) +
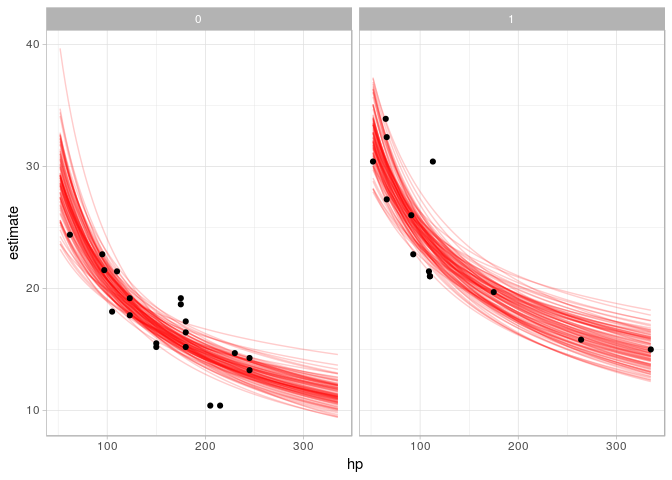
  stat_summary(aes(y = pred), fun.y = median, geom = "line", color = "red", size = 1.25)

Because this is all tidy data, if you wanted to build a model with interactions among different categorical variables (say a different curve for automatic and manual transmissions), you can easily generate predictions faceted over that variable (say, different curves for different transmission types). Then you could use the existing faceting features built in to ggplot to plot them.

Such a model might be:

m_mpg_am = brm(mpg ~ log(hp)*am, data = mtcars, family = lognormal)

Then we can generate and plot predictions as before (differences from above are highlighted as comments):

mtcars %>%
  data_grid(hp = seq_range(hp, n = 101), am) %>%    # add am to the prediction grid
  add_predicted_samples(m_mpg_am) %>%
  ggplot() +
  stat_lineribbon(aes(x = hp, y = pred), .prob = c(.99, .95, .8, .5), inherit.aes = FALSE) +
  geom_point(data = mtcars, aes(x = hp, y = mpg), inherit.aes = FALSE) +
  scale_fill_brewer() +
  facet_wrap(~ am)                                  # facet by am

Or, if you would like overplotted posterior fit lines, you can instead use tidybayes::add_fitted_samples to get samples from fit lines (instead of predictions), select some reasonable number of them (say n = 100), and then plot them:

mtcars %>%
  data_grid(hp = seq_range(hp, n = 101), am) %>%
  add_fitted_samples(m_mpg_am, n = 100) %>%         # sample 100 fits from the posterior
  ggplot() +
  geom_line(aes(x = hp, y = estimate, group = .iteration), alpha = 0.2, color = "red") +
  geom_point(data = mtcars, aes(x = hp, y = mpg), inherit.aes = FALSE) +
  facet_wrap(~ am)

See vignette("tidybayes") for a variety of additional examples and more explanation of how it works.

Feedback, issues, and contributions

I welcome feedback, suggestions, issues, and contributions! Contact me at [email protected]. If you have found a bug, please file it here with minimal code to reproduce the issue. Pull requests should be filed against the dev branch.

tidybayes grew out of helper functions I wrote to make my own analysis pipelines tidier. Over time it has expanded to cover more use cases I have encountered, but I would love to make it cover more!