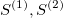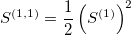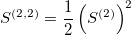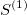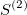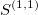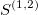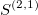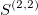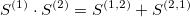What is the signature method?

This repo is dedicated to the theory and practice of the signature method. This is a novel and powerful method for sequential data representation and feature extraction derived from the theory of rough paths in stochastic analysis.

The website is in active stages of development and its content is updated regulary. Stay tuned!

In the meantime, you can explore and familiarise yourself with some recent works in machine learning where the signature method has played a major role.

General overview and real-world examples from the founder of the signature method: Professor Terry Lyons: Rough paths, Signatures and the modelling of functions on streams

A gentle introduction with lots of explained examples and an overview of recent application of the method are concisely represented in: A Primer on the Signature Method in Machine Learning

For mathematical ninjas and those with solid background in statistical machine learning, the next step will be this article: Kernels for sequentially ordered data

Pure mathematicians and audience working with time-series data will highly appreciate this seminal work: Learning from the past, predicting the statistics for the future, learning an evolving system

Here is the collection of real applications of the signature method in different domains:

Deep learning and characters recognition: Sparse arrays of signatures for online character recognition

Finance and stock market: Extracting information from the signature of a financial data stream

Medicine and mental health: Application of the Signature Method to Pattern Recognition in the CEQUEL Clinical Trial

Deep learning and recurrent neural networks: Online Signature Verification using Recurrent Neural Network and Length-normalized Path Signature

Last, but not least, the classic book on the theory of rough paths, it is a collection of lectures given at Saint-Flour school: Differential Equations Driven by Rough Paths

Now let's delve into the Signature Method.

Installation of the ESig package

Practical applications of the signature method (SM) to machine learning and data analysis tasks can be performed using the ESig package. The package is written in C++ with a user-friendly Python wrapper. It is available (however, still in the active stages of development) through a standard command line method:

pip install esig

Also, the package is available at the CoRoPa repository, the ESig-2017-06-07.7z zipped file.

First run

In this tutorial we consider a pragmatic approach to demonstrate the SM at work: starting with practical examples and then moving towards theory. Once you practiced the basics, it will be easier to understand the underlying mathematical foundations and think about future application of the method.

To check the installation, first import the ESig package into your Python session (Here is Python 2.7):

import numpy as np
import esig.tosig as ts

and run a simple example:

two_dim_stream = np.random.random(size=(10,2))
print ts.stream2sig(two_dim_stream, 2)
[1.0, -0.10661163, -0.69629065, 0.00568302, -0.03958541, 0.11381809, 0.242421033]

(the output will depend on your current seed of a random generator and will be different from the presented one, except from the very first term 1, which is always 1 and will be explained below)

A path from ordered data

The key ingredient of the signature method is a path constructed from data. The path is a continuous piece-wise interpolation of data points. For example, consider a collection of pairs 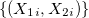, where X_1 = {1,3,5,8} may be thought as time component and X_2 = {1,4,2,6} is a stock price:

Note: For the sake of simplicity and further computational examples, we considered integer numbers only. Of course there is no conceptual restriction to use real numbers. The red dots are discrete data points and the blue solid line is a path continuously connecting the data points. In fact, we took two 1-dimensional sequences and embedded into a single (1-dim) path in 2-dimension. Generalising the idea, any collection of d 1-dim paths can be embedded into a single path in d-dimensions.

The signature is a transformation (mapping) from a path into a collection of real-valued numbers. Each term in the collection has a particular (geometrical) meaning as a function of data points. It is crucial to understand each term in the resulting signature. The general form of the signatures is given by iterated integrals (projections or coordinates) of a path. For example, the signature truncated at level (depth) L=2, has a form: 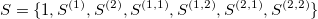, where:

• 1 - is the first term and always equals to 1 (zeroth-order approximation)
• - linear terms, correspond to the total increment (net Euclidean distance between the end points along each dimension)
• - a square of the first linear term term (with a factor 1/2)
• - second order approximations (areas under the path computed
• - a square of the second linear term (with a factor 1/2)

and these areas are presented in the following figure:

The path presented in above is obtained by running the code:

import numpy as np
import esig.tosig as ts
X_1 = np.array([1., 3., 5., 8.]).reshape((-1,1))
X_2 = np.array([1., 4., 2., 6.]).reshape((-1,1))
two_dim_stream = np.append(X_1,X_2, axis=1)
signatures = ts.stream2sig(two_dim_stream, 2)
print signatures
>> [1., 7., 5., 24.5., 19., 16., 12.5]

where:

• = 7.
• = 5.
• = 24.5
• = 19.
• = 16.
• = 12.5

One can easily compute coloured areas 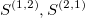from the plots and compare to numerical values of the corresponding signature terms.

Shuffle product

One of the most important property of the signature terms (signatures), which stems from the algebra of the iterated integrals, is the shuffle product. The shuffle product allows to represent any product (polynomial) of the signature terms as a linear combination of the higher-order terms. For example:

which also could be verified numerically.

Important:

the input array should always be in the form: length_of_stream x dimension_of_stream. For example, two dimensional array consisting of 4 points, should be reshaped as 4x2 array (rows are data points and columns are unique streams).

Bookkeeping:

For the sake of consistency, we denote the input data size and the signature truncation parameter by:

• p - number of rows (data points)
• q - number of streams (unidimensional sequences)
• L - signature truncation level (depth)

Functions of the ESig package

Two main transformations (log and full signature) are given by:

• ts.stream2logsig(data, L)
• ts.stream2sig(data, L)

where the functions receive two arguments, were data - is a numpy array (your data) of size p x q and as defined earlier L - the signature truncation level.

The esig package contains a handy help option, which explains on the available methods. Briefly, they are:

• ts.logsigdim(q, L) - computes the size of the feature set given by log-signature.

three_dim_stream = np.random.random(size=(100,3))
print ts.logsigdim(three_dim_stream.shape[1], 4)
>> 32

which is a size of the feature set given by this three dimensional stream computed up to level 4 of the truncated signature. Similar function computes the size of the resulting feature set, but for the full (exponentiated) signature:

• ts.sigdim(q, L) - computes the size of the feature set given by the full signature.

three_dim_stream = np.random.random(size=(100,3))
print ts.sigdim(three_dim_stream.shape[1], 4)
>> 121

• ts.sigkeys(q, L) - outputs the combination of 'letters', or ordering of the iterated integrals of the full signature.

two_dim_stream = np.random.random(size=(100,2))
print ts.sigkeys(two_dim_stream.shape[1], 2)
>> (), (1), (2), (1,1), (1,2), (2,1), (2,2)

By comparing this expression to the general form of the signature of two dimensional stream truncated at level 2 given in above, one can easily see the correspondence between the terms.

Examples

(coming soon...)