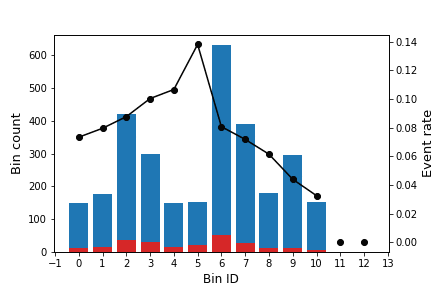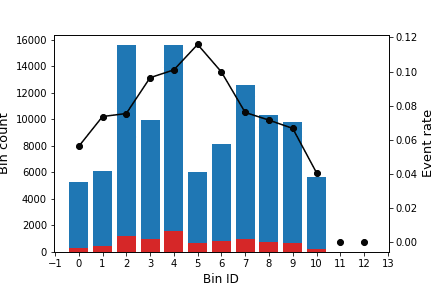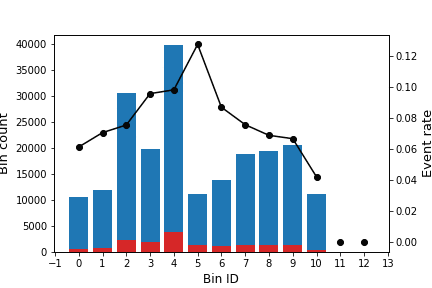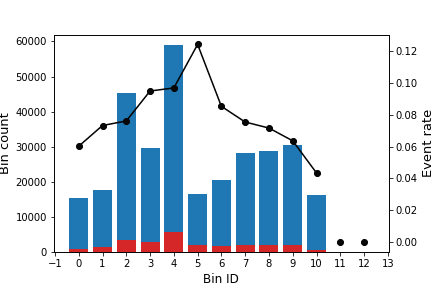
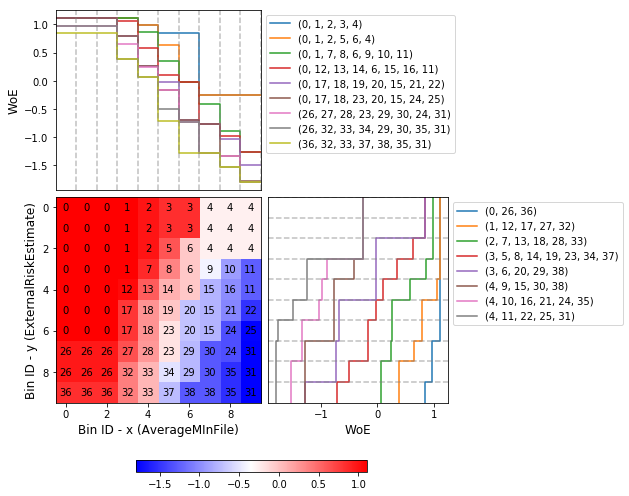
OptBinning is a library written in Python implementing a rigorous and flexible mathematical programming formulation to solve the optimal binning problem for a binary, continuous and multiclass target type, incorporating constraints not previously addressed.
- Papers:
- Optimal binning: mathematical programming formulation. http://arxiv.org/abs/2001.08025
- Optimal counterfactual explanations for scorecard modelling. https://arxiv.org/abs/2104.08619
- Blog: Optimal binning for streaming data. http://gnpalencia.org/blog/2020/binning_data_streams/
Table of Contents
To install the current release of OptBinning from PyPI:
pip install optbinning
To include batch and stream binning algorithms (this option is not required for most users):
pip install optbinning[distributed]
To install from source, download or clone the git repository
git clone https://github.com/guillermo-navas-palencia/optbinning.git
cd optbinning
python setup.py install
OptBinning requires
- matplotlib
- numpy (>=1.16.1)
- ortools (>=9.4)
- pandas
- ropwr (>=1.0.0)
- scikit-learn (>=1.0.2)
- scipy (>=1.6.0)
OptBinning[distributed] requires additional packages
- pympler
- tdigest
Please visit the OptBinning documentation (current release) http://gnpalencia.org/optbinning/. If your are new to OptBinning, you can get started following the tutorials and checking the API references.
- Optimal binning tutorials
- Binning process tutorials
- Scorecard and counterfactual tutorials
- Optimal piecewise binning tutorials
- Batch and stream optimal binning tutorials
- Optimal binning under uncertainty
- Optimal binning 2D
Let's load a well-known dataset from the UCI repository and choose a variable to discretize and the binary target.
import pandas as pd
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
df = pd.DataFrame(data.data, columns=data.feature_names)
variable = "mean radius"
x = df[variable].values
y = data.targetImport and instantiate an OptimalBinning object class. We pass the variable name, its data type, and a solver, in this case, we choose the constraint programming solver. Fit the optimal binning object with arrays x and y.
from optbinning import OptimalBinning
optb = OptimalBinning(name=variable, dtype="numerical", solver="cp")
optb.fit(x, y)Check status and retrieve optimal split points
>>> optb.status
'OPTIMAL'
>>> optb.splits
array([11.42500019, 12.32999992, 13.09499979, 13.70499992, 15.04500008,
16.92500019])The optimal binning algorithms return a binning table; a binning table displays the binned data and several metrics for each bin. Call the method build, which returns a pandas.DataFrame.
>>> optb.binning_table.build() Bin Count Count (%) Non-event Event Event rate WoE IV JS
0 [-inf, 11.43) 118 0.207381 3 115 0.974576 -3.12517 0.962483 0.087205
1 [11.43, 12.33) 79 0.138840 3 76 0.962025 -2.71097 0.538763 0.052198
2 [12.33, 13.09) 68 0.119508 7 61 0.897059 -1.64381 0.226599 0.025513
3 [13.09, 13.70) 49 0.086116 10 39 0.795918 -0.839827 0.052131 0.006331
4 [13.70, 15.05) 83 0.145870 28 55 0.662651 -0.153979 0.003385 0.000423
5 [15.05, 16.93) 54 0.094903 44 10 0.185185 2.00275 0.359566 0.038678
6 [16.93, inf) 118 0.207381 117 1 0.008475 5.28332 2.900997 0.183436
7 Special 0 0.000000 0 0 0.000000 0 0.000000 0.000000
8 Missing 0 0.000000 0 0 0.000000 0 0.000000 0.000000
Totals 569 1.000000 212 357 0.627417 5.043925 0.393784
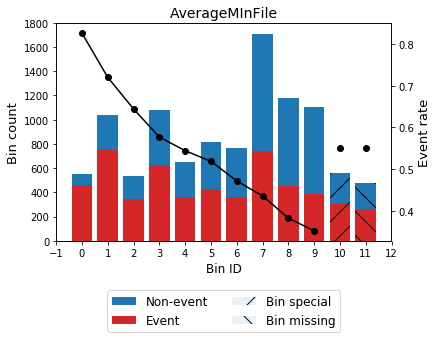
You can use the method plot to visualize the histogram and WoE or event rate curve. Note that the Bin ID corresponds to the binning table index.
>>> optb.binning_table.plot(metric="woe")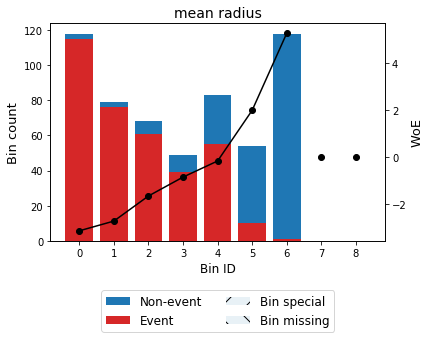
Optionally, you can show the binning plot with the actual bin widths.
>>> optb.binning_table.plot(metric="woe", style="actual", add_special=False, add_missing=False)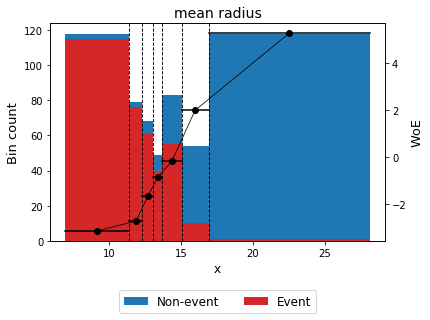
Now that we have checked the binned data, we can transform our original data into WoE or event rate values.
x_transform_woe = optb.transform(x, metric="woe")
x_transform_event_rate = optb.transform(x, metric="event_rate")The analysis method performs a statistical analysis of the binning table, computing the statistics Gini index, Information Value (IV), Jensen-Shannon divergence, and the quality score. Additionally, several statistical significance tests between consecutive bins of the contingency table are performed.
>>> optb.binning_table.analysis()---------------------------------------------
OptimalBinning: Binary Binning Table Analysis
---------------------------------------------
General metrics
Gini index 0.87541620
IV (Jeffrey) 5.04392547
JS (Jensen-Shannon) 0.39378376
Hellinger 0.47248971
Triangular 1.25592041
KS 0.72862164
HHI 0.15727342
HHI (normalized) 0.05193260
Cramer's V 0.80066760
Quality score 0.00000000
Monotonic trend descending
Significance tests
Bin A Bin B t-statistic p-value P[A > B] P[B > A]
0 1 0.252432 6.153679e-01 0.684380 3.156202e-01
1 2 2.432829 1.188183e-01 0.948125 5.187465e-02
2 3 2.345804 1.256207e-01 0.937874 6.212635e-02
3 4 2.669235 1.023052e-01 0.955269 4.473083e-02
4 5 29.910964 4.523477e-08 1.000000 9.814594e-12
5 6 19.324617 1.102754e-05 0.999999 1.216668e-06
Print overview information about the options settings, problem statistics, and the solution of the computation.
>>> optb.information(print_level=2)optbinning (Version 0.17.3)
Copyright (c) 2019-2023 Guillermo Navas-Palencia, Apache License 2.0
Begin options
name mean radius * U
dtype numerical * d
prebinning_method cart * d
solver cp * d
divergence iv * d
max_n_prebins 20 * d
min_prebin_size 0.05 * d
min_n_bins no * d
max_n_bins no * d
min_bin_size no * d
max_bin_size no * d
min_bin_n_nonevent no * d
max_bin_n_nonevent no * d
min_bin_n_event no * d
max_bin_n_event no * d
monotonic_trend auto * d
min_event_rate_diff 0 * d
max_pvalue no * d
max_pvalue_policy consecutive * d
gamma 0 * d
class_weight no * d
cat_cutoff no * d
user_splits no * d
user_splits_fixed no * d
special_codes no * d
split_digits no * d
mip_solver bop * d
time_limit 100 * d
verbose False * d
End options
Name : mean radius
Status : OPTIMAL
Pre-binning statistics
Number of pre-bins 9
Number of refinements 1
Solver statistics
Type cp
Number of booleans 26
Number of branches 58
Number of conflicts 0
Objective value 5043922
Best objective bound 5043922
Timing
Total time 0.04 sec
Pre-processing 0.00 sec ( 0.33%)
Pre-binning 0.00 sec ( 5.54%)
Solver 0.04 sec ( 93.03%)
model generation 0.03 sec ( 85.61%)
optimizer 0.01 sec ( 14.39%)
Post-processing 0.00 sec ( 0.30%)
In this case, we choose two variables to discretized and the binary target.
import pandas as pd
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
df = pd.DataFrame(data.data, columns=data.feature_names)
variable1 = "mean radius"
variable2 = "worst concavity"
x = df[variable1].values
y = df[variable2].values
z = data.targetImport and instantiate an OptimalBinning2D object class. We pass the variable names, and monotonic trends. Fit the optimal binning object with arrays x, y and z.
from optbinning import OptimalBinning2D
optb = OptimalBinning2D(name_x=variable1, name_y=variable2, monotonic_trend_x="descending",
monotonic_trend_y="descending", min_bin_size=0.05)
optb.fit(x, y, z)Show binning table:
>>> optb.binning_table.build() Bin x Bin y Count Count (%) Non-event Event Event rate WoE IV JS
0 (-inf, 13.70) (-inf, 0.21) 219 0.384886 1 218 0.995434 -4.863346 2.946834 0.199430
1 [13.70, inf) (-inf, 0.21) 48 0.084359 5 43 0.895833 -1.630613 0.157946 0.017811
2 (-inf, 13.09) [0.21, 0.38) 48 0.084359 1 47 0.979167 -3.328998 0.422569 0.037010
3 [13.09, 15.05) [0.21, 0.38) 46 0.080844 17 29 0.630435 -0.012933 0.000013 0.000002
4 [15.05, inf) [0.21, 0.32) 32 0.056239 29 3 0.093750 2.789833 0.358184 0.034271
5 [15.05, inf) [0.32, inf) 129 0.226714 128 1 0.007752 5.373180 3.229133 0.201294
6 (-inf, 15.05) [0.38, inf) 47 0.082601 31 16 0.340426 1.182548 0.119920 0.014173
7 Special Special 0 0.000000 0 0 0.000000 0.000000 0.000000 0.000000
8 Missing Missing 0 0.000000 0 0 0.000000 0.000000 0.000000 0.000000
Totals 569 1.000000 212 357 0.627417 7.234600 0.503991
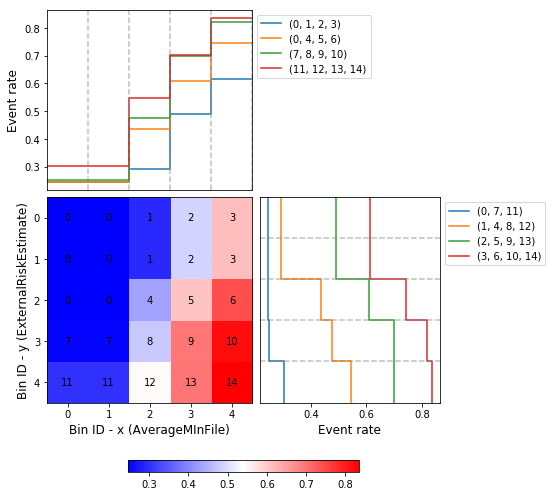
Similar to the optimal binning, you can generate a histogram 2D to visualize WoE and event rate.
>>> optb.binning_table.plot(metric="event_rate")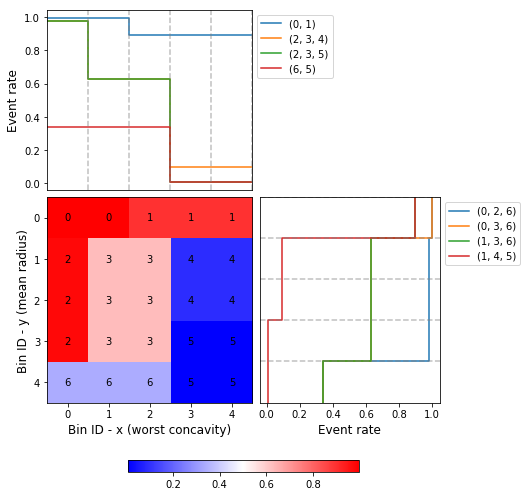
Let's load the California housing dataset.
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import HuberRegressor
from optbinning import BinningProcess
from optbinning import Scorecard
data = fetch_california_housing()
target = "target"
variable_names = data.feature_names
X = pd.DataFrame(data.data, columns=variable_names)
y = data.targetInstantiate a binning process, an estimator, and a scorecard with scaling method and reverse mode.
binning_process = BinningProcess(variable_names)
estimator = HuberRegressor(max_iter=200)
scorecard = Scorecard(binning_process=binning_process, estimator=estimator,
scaling_method="min_max",
scaling_method_params={"min": 0, "max": 100},
reverse_scorecard=True)
scorecard.fit(X, y)Print overview information about the options settings, problems statistics, and the number of selected variables after the binning process.
>>> scorecard.information(print_level=2)optbinning (Version 0.17.3)
Copyright (c) 2019-2023 Guillermo Navas-Palencia, Apache License 2.0
Begin options
binning_process yes * U
estimator yes * U
scaling_method min_max * U
scaling_method_params yes * U
intercept_based False * d
reverse_scorecard True * U
rounding False * d
verbose False * d
End options
Statistics
Number of records 20640
Number of variables 8
Target type continuous
Number of numerical 8
Number of categorical 0
Number of selected 8
Timing
Total time 2.31 sec
Binning process 1.83 sec ( 79.00%)
Estimator 0.41 sec ( 17.52%)
Build scorecard 0.08 sec ( 3.40%)
rounding 0.00 sec ( 0.00%)
>>> scorecard.table(style="summary")Two scorecard styles are available: style="summary" shows the variable name, and their corresponding bins and assigned points; style="detailed" adds information from the corresponding binning table.
Variable Bin Points
0 MedInc [-inf, 1.90) 9.869224
1 MedInc [1.90, 2.16) 10.896940
2 MedInc [2.16, 2.37) 11.482997
3 MedInc [2.37, 2.66) 12.607805
4 MedInc [2.66, 2.88) 13.609078
.. ... ... ...
2 Longitude [-118.33, -118.26) 10.470401
3 Longitude [-118.26, -118.16) 9.092391
4 Longitude [-118.16, inf) 10.223936
5 Longitude Special 1.376862
6 Longitude Missing 1.376862
[94 rows x 3 columns]
>>> scorecard.table(style="detailed") Variable Bin id Bin Count Count (%) ... Zeros count WoE IV Coefficient Points
0 MedInc 0 [-inf, 1.90) 2039 0.098789 ... 0 -0.969609 0.095786 0.990122 9.869224
1 MedInc 1 [1.90, 2.16) 1109 0.053731 ... 0 -0.836618 0.044952 0.990122 10.896940
2 MedInc 2 [2.16, 2.37) 1049 0.050824 ... 0 -0.760779 0.038666 0.990122 11.482997
3 MedInc 3 [2.37, 2.66) 1551 0.075145 ... 0 -0.615224 0.046231 0.990122 12.607805
4 MedInc 4 [2.66, 2.88) 1075 0.052083 ... 0 -0.485655 0.025295 0.990122 13.609078
.. ... ... ... ... ... ... ... ... ... ... ...
2 Longitude 2 [-118.33, -118.26) 1120 0.054264 ... 0 -0.011006 0.000597 0.566265 10.470401
3 Longitude 3 [-118.26, -118.16) 1127 0.054603 ... 0 -0.322802 0.017626 0.566265 9.092391
4 Longitude 4 [-118.16, inf) 6530 0.316376 ... 0 -0.066773 0.021125 0.566265 10.223936
5 Longitude 5 Special 0 0.000000 ... 0 -2.068558 0.000000 0.566265 1.376862
6 Longitude 6 Missing 0 0.000000 ... 0 -2.068558 0.000000 0.566265 1.376862
[94 rows x 14 columns]
Compute score and predicted target using the fitted estimator.
score = scorecard.score(X)
y_pred = scorecard.predict(X)First, we load the dataset and a scorecard previously developed.
import pandas as pd
from optbinning import Scorecard
from optbinning.scorecard import Counterfactual
from sklearn.datasets import load_boston
data = load_boston()
X = pd.DataFrame(data.data, columns=data.feature_names)
scorecard = Scorecard.load("myscorecard.pkl")We create a new Counterfactual instance that is fitted with the dataset used during the scorecard development. Then, we select a sample from which to generate counterfactual explanations.
cf = Counterfactual(scorecard=scorecard)
cf.fit(X)
query = X.iloc[0, :].to_frame().TThe scorecard model predicts 26.8. However, we would like to find out what needs to be changed to return a prediction greater or equal to 30.
>>> query
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT
0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.09 1.0 296.0 15.3 396.9 4.98
>>> scorecard.predict(query)
array([26.83423364])We can generate a single counterfactual explanation:
>>> cf.generate(query=query, y=30, outcome_type="continuous", n_cf=1, max_changes=3,
hard_constraints=["min_outcome"])
>>> cf.status
'OPTIMAL'
>>> cf.display(show_only_changes=True, show_outcome=True)
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT outcome
0 [0.04, 0.07) - - - [0.45, 0.50) [6.94, 7.44) - - - - - - - 31.28763Or simultaneously three counterfactuals, enforcing diversity on the feature values and selecting only a few actionable features.
>>> cf.generate(query=query, y=30, outcome_type="continuous", n_cf=3, max_changes=3,
hard_constraints=["diversity_values", "min_outcome"],
actionable_features=["CRIM", "NOX", "RM", "PTRATIO"])
>>> cf.status
'OPTIMAL'
>>> cf.display(show_only_changes=True, show_outcome=True)
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT outcome
0 [0.03, 0.04) - - - [0.42, 0.45) [6.94, 7.44) - - - - - - - 31.737844
0 [0.04, 0.07) - - - - [7.44, inf) - - - - [17.85, 18.55) - - 36.370086
0 - - - - [0.45, 0.50) [6.68, 6.94) - - - - [-inf, 15.15) - - 30.095258The following table shows how OptBinning compares to scorecardpy 0.1.9.1.1 on a selection of variables from the public dataset, Home Credit Default Risk - Kaggle’s competition Link. This dataset contains 307511 samples.The experiments were run on Intel(R) Core(TM) i5-3317 CPU at 1.70GHz, using a single core, running Linux. For scorecardpy, we use default settings only increasing the maximum number of bins bin_num_limit=20. For OptBinning, we use default settings (max_n_prebins=20) only changing the maximum allowed p-value between consecutive bins, max_pvalue=0.05.
To compare softwares we use the shifted geometric mean, typically used in mathematical optimization benchmarks: http://plato.asu.edu/bench.html. Using the shifted (by 1 second) geometric mean we found that OptBinning is 17x faster than scorecardpy, with an average IV increment of 12%. Besides the speed and IV gains, OptBinning includes many more constraints and monotonicity options.
| Variable | scorecardpy_time | scorecardpy_IV | optbinning_time | optbinning_IV |
|---|---|---|---|---|
| AMT_INCOME_TOTAL | 6.18 s | 0.010606 | 0.363 s | 0.011705 |
| NAME_CONTRACT_TYPE (C) | 3.72 s | 0.015039 | 0.148 s | 0.015039 |
| AMT_CREDIT | 7.10 s | 0.053593 | 0.634 s | 0.059311 |
| ORGANIZATION_TYPE (C) | 6.31 s | 0.063098 | 0.274 s | 0.071520 |
| AMT_ANNUITY | 6.51 s | 0.024295 | 0.648 s | 0.031179 |
| AMT_GOODS_PRICE | 6.95 s | 0.056923 | 0.401 s | 0.092032 |
| NAME_HOUSING_TYPE (C) | 3.57 s | 0.015055 | 0.140 s | 0.015055 |
| REGION_POPULATION_RELATIVE | 4.33 s | 0.026578 | 0.392 s | 0.035567 |
| DAYS_BIRTH | 5.18 s | 0.081270 | 0.564 s | 0.086539 |
| OWN_CAR_AGE | 4.85 s | 0.021429 | 0.055 s | 0.021890 |
| OCCUPATION_TYPE (C) | 4.24 s | 0.077606 | 0.201 s | 0.079540 |
| APARTMENTS_AVG | 5.61 s | 0.032247(*) | 0.184 s | 0.032415 |
| BASEMENTAREA_AVG | 5.14 s | 0.022320 | 0.119 s | 0.022639 |
| YEARS_BUILD_AVG | 4.49 s | 0.016033 | 0.055 s | 0.016932 |
| EXT_SOURCE_2 | 5.21 s | 0.298463 | 0.606 s | 0.321417 |
| EXT_SOURCE_3 | 5.08 s | 0.316352 | 0.303 s | 0.334975 |
| TOTAL | 84.47 s | 1.130907 | 5.087 s | 1.247756 |
(C): categorical variable. (*): max p-value between consecutive bins > 0.05.
The binning of variables with monotonicity trend peak or valley can benefit from the option monotonic_trend="auto_heuristic" at the expense of finding a suboptimal solution for some cases. The following table compares the options monotonic_trend="auto" and monotonic_trend="auto_heuristic",
| Variable | auto_time | auto_IV | heuristic_time | heuristic_IV |
|---|---|---|---|---|
| AMT_INCOME_TOTAL | 0.363 s | 0.011705 | 0.322 s | 0.011705 |
| AMT_CREDIT | 0.634 s | 0.059311 | 0.469 s | 0.058643 |
| AMT_ANNUITY | 0.648 s | 0.031179 | 0.505 s | 0.031179 |
| AMT_GOODS_PRICE | 0.401 s | 0.092032 | 0.299 s | 0.092032 |
| REGION_POPULATION_RELATIVE | 0.392 s | 0.035567 | 0.244 s | 0.035567 |
| TOTAL | 2.438 s | 0.229794 | 1.839 s | 0.229126 |
Observe that CPU time is reduced by 25% losing less than 1% in IV. The differences in CPU time are more noticeable as the number of bins increases, see http://gnpalencia.org/optbinning/tutorials/tutorial_binary_large_scale.html.
Found a bug? Want to contribute with a new feature, improve documentation, or add examples? We encourage you to create pull requests and/or open GitHub issues. Thanks! ![]() 🎉 👍
🎉 👍
We would like to list companies using OptBinning. Please send a PR with your company name and @githubhandle if you may.
Currently officially using OptBinning:
- Jeitto [@BrennerPablo & @ds-mauri & @GabrielSGoncalves]
- Bilendo [@FlorianKappert & @JakobBeyer]
- Aplazame
- Praelexis Credit
- ING
- DBRS Morningstar
- Loginom
- Risika
- Tamara
- BBVA AI Factory
- N26
- Home Credit International
- Farm Credit Canada
If you use OptBinning in your research/work, please cite the paper using the following BibTeX:
@article{Navas-Palencia2020OptBinning,
title = {Optimal binning: mathematical programming formulation},
author = {Guillermo Navas-Palencia},
year = {2020},
eprint = {2001.08025},
archivePrefix = {arXiv},
primaryClass = {cs.LG},
volume = {abs/2001.08025},
url = {http://arxiv.org/abs/2001.08025},
}
@article{Navas-Palencia2021Counterfactual,
title = {Optimal Counterfactual Explanations for Scorecard modelling},
author = {Guillermo Navas-Palencia},
year = {2021},
eprint = {2104.08619},
archivePrefix = {arXiv},
primaryClass = {cs.LG},
volume = {abs/2104.08619},
url = {http://arxiv.org/abs/2104.08619},
}