- Debe recibir como entrada un número primo p, de cualquier tamaño (por ejemplo los recomendados para aplicaciones criptográficas (1024,2048,.. bits)
- Construir un Grupo multiplicativo
$Zp^{*}$ (usando el conjunto${1,2,...p-1}$ y la operación $ \star mod p$ - Usar como generador algún elemento aleatorio de
$Zp^{*}$ - Usando ElGamal, se deberán generar dos parejas de llaves con el algoritmo
$ElGamal.keyGen()$ - Realizar lo siguiente:
- Generar una cadena de caracteres
$s = [c1,c2,c3...cn]$ tal que su longitud en bits es menor a la longitud de p - Cifra s, esto es: calcula
$x \leftarrow ElGamal.encrypts(s,X_{B})$ - Envia c a B
- Generar una cadena de caracteres
- Cuando B recibe c, realiza lo siguiente
- Descifra c, calculando
$s \leftarrow ElGamal.decrypt(c,X_{B})$ - Calcula
$s' = [cn...c3,c2,c1]$ - Cifra s', esto es, calcula
$c' \leftarrow ElGamal.encrypt(s',X_{A})$ - Envia c' a A
- Descifra c, calculando
- Cuando A recibe c', descifra para obtener s', y verifica que si
$s' = [cn...c3,c2,c1]$ - Se deberán ejecutar los pasos 4-7 en al menos 10 casos de prueba, usando un valor de p diferente para cada caso, siendo que p puede ser de entre 1024 y 2048 bits.
- Reportar en una tabla de tiempos la ejecución para cada caso de prueba.
- Eje X: Nivel de seguridad (tamaño en bits de p)
- Eje Y: tiempo de ejecución de los pasos 4-7
El proyecto está escrito en lenguaje python3.8 (el cual no es muy recomendable para aplicaciones donde se espera un mejor "performance") con ayuda de la libreria pycryptodome
Tener la versión >= python3.
Instalar las dependencias marcadas bajo el comando
pip install <nombre_paquete>Dependencias
* cryptography = "^38.0.1"
* pycryptodome = "^3.15.0"
* pycryptodomex = "^3.15.0"
* matplotlib = "^3.6.0"
* tabulate = "^0.8.10"
Se cuenta una versión funcional del laboratorio en la plataforma replit. (Se debe de contar con una cuenta) Debido a que es una cuenta gratuita los resultados son limitados, pero funcionales.
https://replit.com/join/szodbvyxqb-luisballado
Arreglo de bits usados
bits = [1024,1128,1232,1336,1440,1544,1648,1752,1856,1960,2048]Con uso de la libreria matplotlib a partir de los datos generados
def graficar(x_datos,y_datos,result_arr):
print(tabulate(result_arr))
x1 = np.array(x_datos)
y1 = np.array(y_datos)
plt.plot(x1, y1, marker="o")
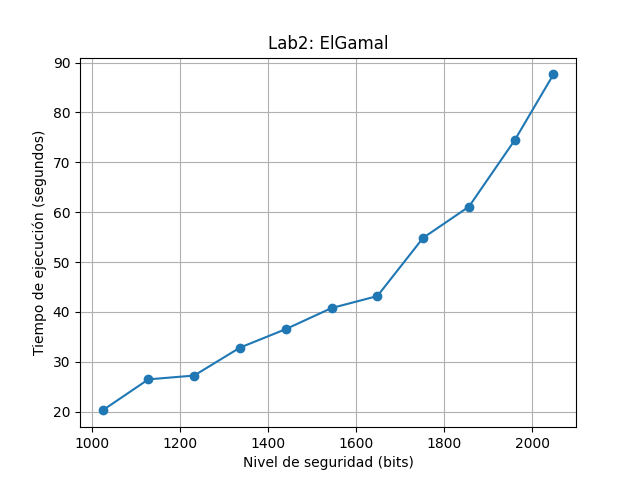
plt.title("Lab2: ElGamal")
plt.xlabel("Nivel de seguridad (bits)")
plt.ylabel("Tiempo de ejecución (segundos)")
plt.grid()
plt.show()def generar_palabras(longitud):
letters = string.ascii_uppercase
return ''.join(random.choice(letters) for i in range(longitud))def inv_palabra(palabra):
return palabra[::-1]if inv_palabra(msg) == inv_palabra(dmsg):
print("Son iguales")
else:
print("No iguales")Tomando en cuenta que la ejecución se realizó en replit con una máquina de baja caracteristicas, se puede observar que a medida que se incrementa la dificultad en la generación del número primo p en base a los bits, el tiempo de ejecución aumenta exponencialmente.
| Bits | Segundos |
|---|---|
| 1024 | 20.2473 |
| 1128 | 26.4697 |
| 1232 | 27.2355 |
| 1336 | 32.8339 |
| 1440 | 36.5402 |
| 1544 | 40.7695 |
| 1648 | 43.1699 |
| 1752 | 54.8489 |
| 1856 | 61.1026 |
| 1960 | 74.4333 |
| 2048 | 87.6311 |