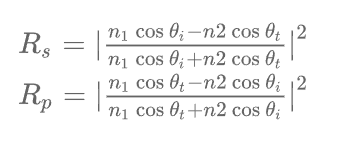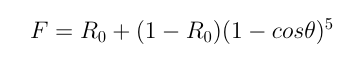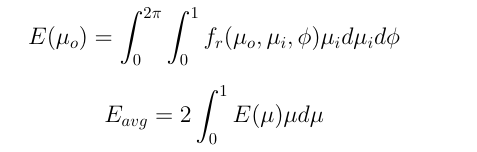会用到的库函数
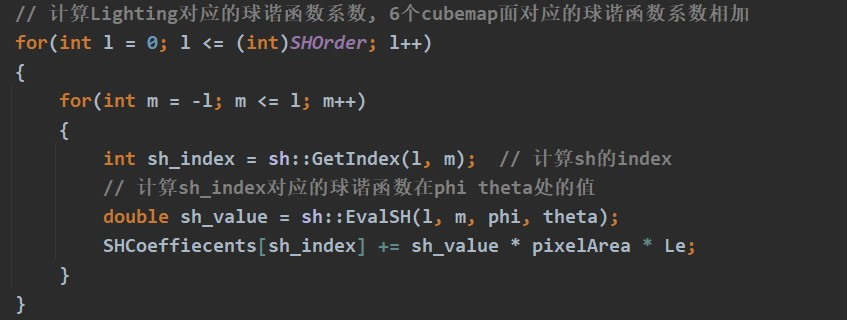
sh::ToSphericalCoords(const Eigen::Vector3d& dir, double* phi, double* theta) -> void 将笛卡尔坐标系下的向量转为球面坐标系方向 sh::GetIndex(int l, int m) -> int 计算l阶的m球谐函数对应的index sh::EvalSH(int l, int m, double phi, double theta) -> double 计算l, m对应的球谐函数在theta, phi方向的值
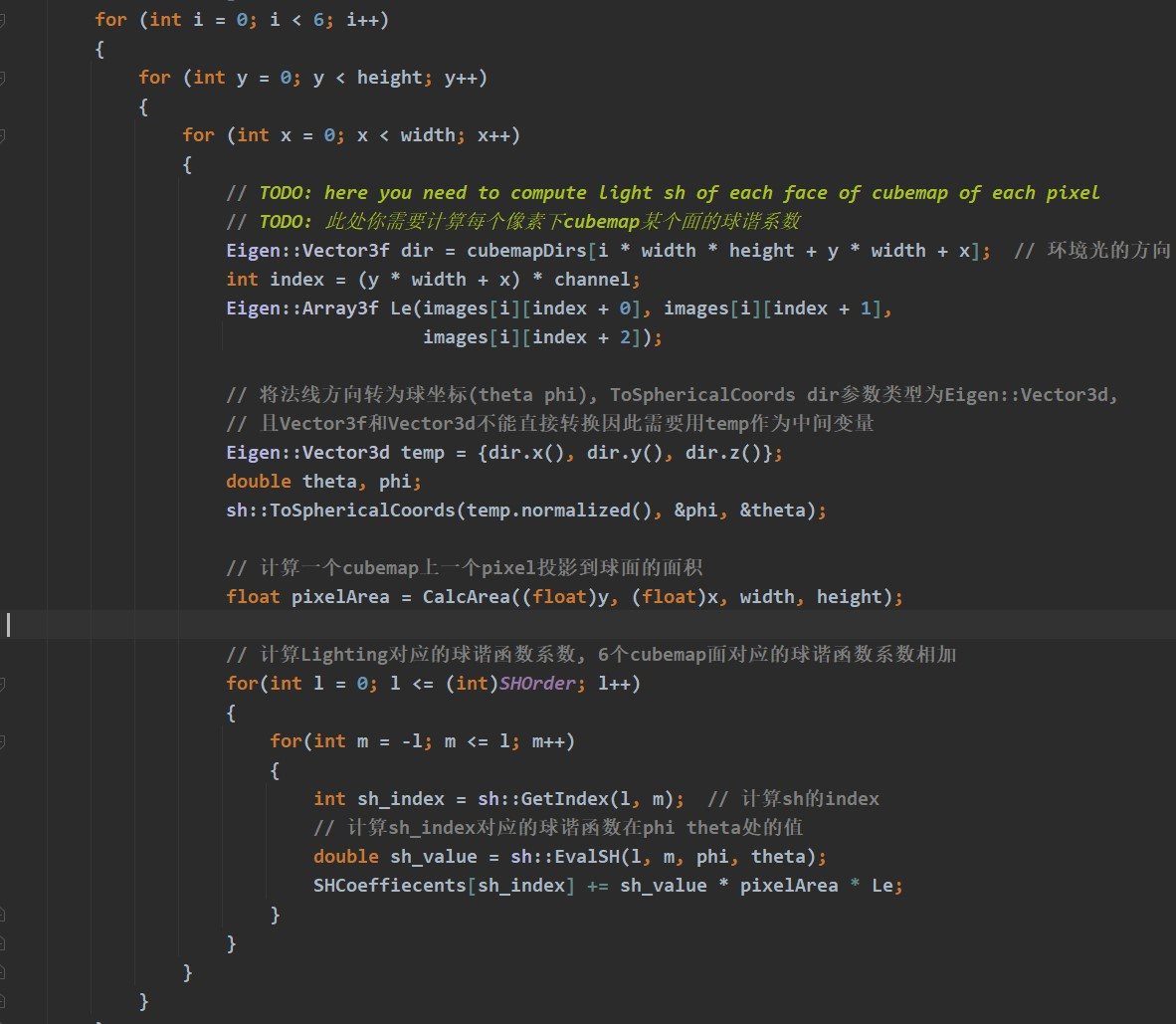
首先将cubemap的某个像素下的光照方向转为球面坐标(theta, phi), 注意需要将temp单位化
计算cubemap上一个pixel对应球面上的面积
SH的系数为环境光Le与SH basis的乘积在半球空间上的积分,这里用求和的形式,对于每一个piexl计算一次分量然后求和
完整代码
最外层循环将cubemap的6个面对应的SH各阶系数同存储在SHCoeffiecents中,接下来的两次循环遍历一张cubemap的像素,计算该像素对SH basis系数的贡献,可以理解为计算cubemap的一个面展开为SH basis对应的系数
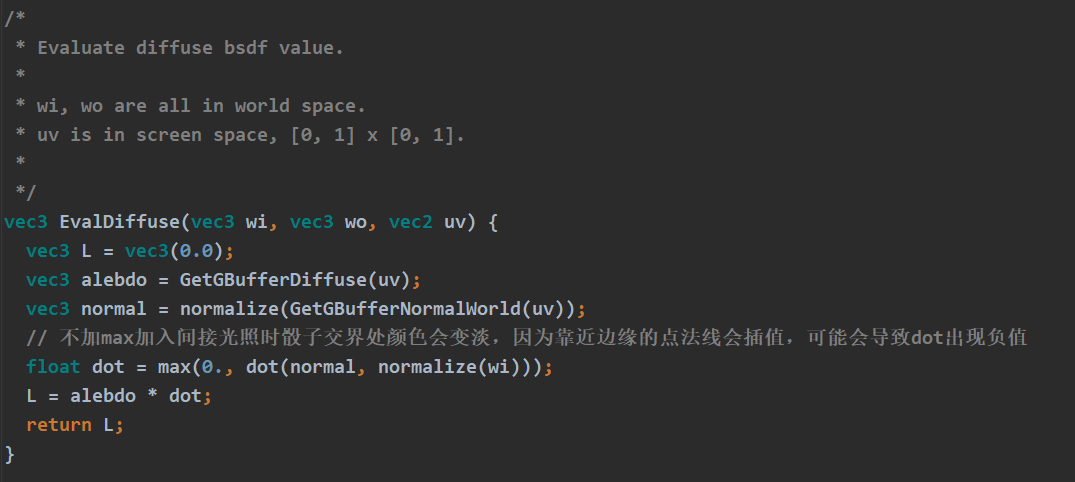
对于diffuse材质的物体,不考虑visibility,LightTransport项可以化简为$\frac{\rho}{\pi}$max(n$\cdot$i, 0)
只需要在匿名函数shFunc中计算LightTransport在给定方向(theta, phi)下的值即可,Diffuse Unshadowed只需返回max(n$\cdot$i, 0)
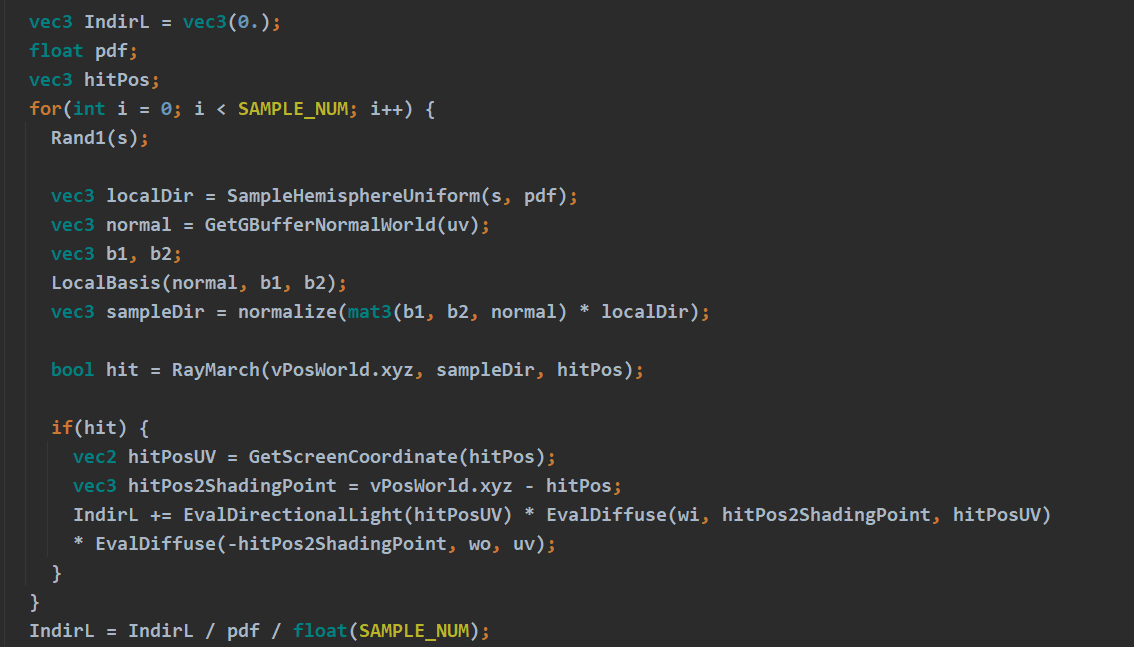
Lighting部分之所以不用consine term采样的方法做是因为通过随机采样$w_i$不好计算其与cube map的交点(如果做的话需要做射线与平面求交,还需要进行插值处理),进而得不到入射的radiance。
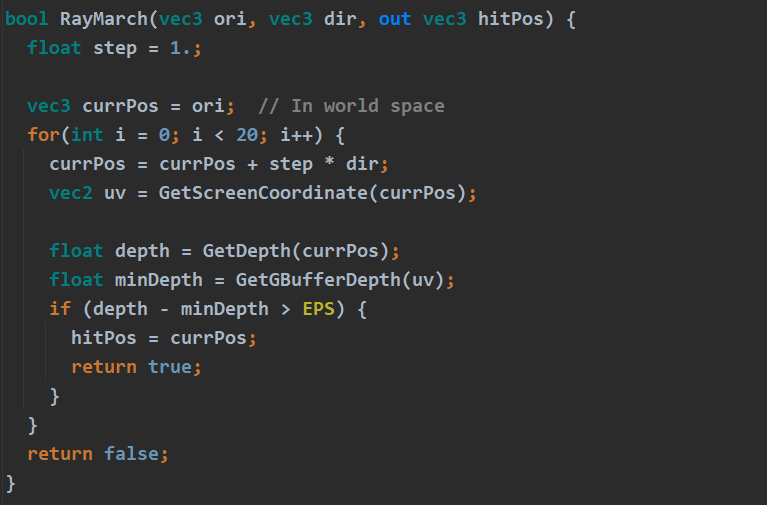
与Unshadowed相比多了visibility项,从shading point向wi发射一条ray判断是否与场景相交
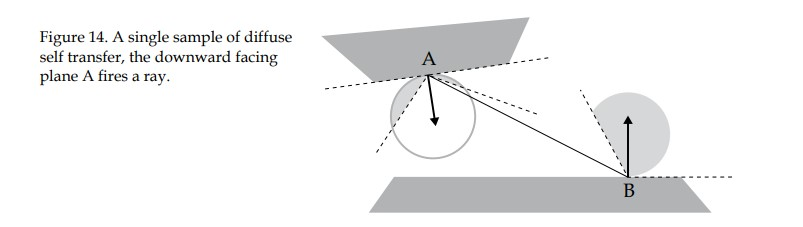
基本思想:如何计算一个vertex的间接Light Transport?
从该vertex发射一条ray(direction为wi),如果ray与空间中的三角形相交,由于光线可逆,这个交点会向vertex发射radiance,用barycentric intepolation计算交点的SH Coefficients,那么交点对vertex SH Coeffs的贡献为交点的SH Coeffs乘上cosine term(dot(wi, vertex的normal))。
写一个递归函数来计算每个点Indirect Light Transport即可,最后将Indir的LT加到Dir的LT上,记住Indir LT不要忘记乘上$\frac{1}{\pi}$。
球谐函数的两个重要性质:
-
旋转不变性;
-
对于每一个band上的SH Coeffs,其旋转后的SH Coeffs都可以被同band上的SH Coeffs线性表示。
由于性质1我们求旋转后的天空盒函数投影到SH的系数可以转换为求天空盒函数投影到SH上的系数得旋转矩阵,由于性质2旋转SH Coeffs是线性变换 $$ 取l\ band上的2l+1个向量n_i\ R(P(n_i)) = P(R(n_i))\ \ \ 性质1\ R(P(n_i)) = MP(n_i)\ \ \ 性质2\ 因此有\M(P(n_i)) = P(R(n_i)) $$ 为什么要利用性质1转换成先旋转再投影,个人理解是先投影的话SH Coeffs向量过长(l=3 向量长度为9),无法直接用3阶(4阶)的旋转矩阵作用在向量上。
- 自己新建材质的js文件需要手动在index.html中进行加载,否则加载不出mary模型;
- tools.js中的mat4Matrix2mathMatrix函数未考虑行列优先的不同,glMatrix是列优先,math.js是行优先,因此此函数返回值需要transpose,同样,在WebRenderer.js中将旋转后的PrecomputeL_RGB3是行优先(9 * 3), 传入uniform时需要转置;
- 在WebGLRenderer.js line55注释中将rotationMatrix解释为天空盒的旋转矩阵, 但是实际是作用于物体上的, 是物体的旋转矩阵, 对应的天空盒旋转矩阵为rotationMatrix的逆矩阵。
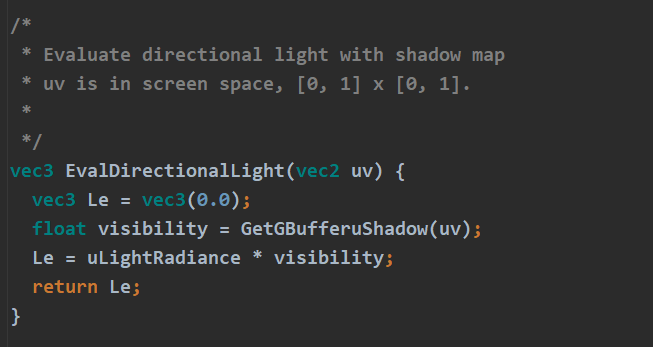
Incident radiance + visibility
BSDF: diffuse材质,首先读取GBuffer中的diffuse对应的albedo,然后乘上cosine term
for循环的上限决定搜索hitPos的范围
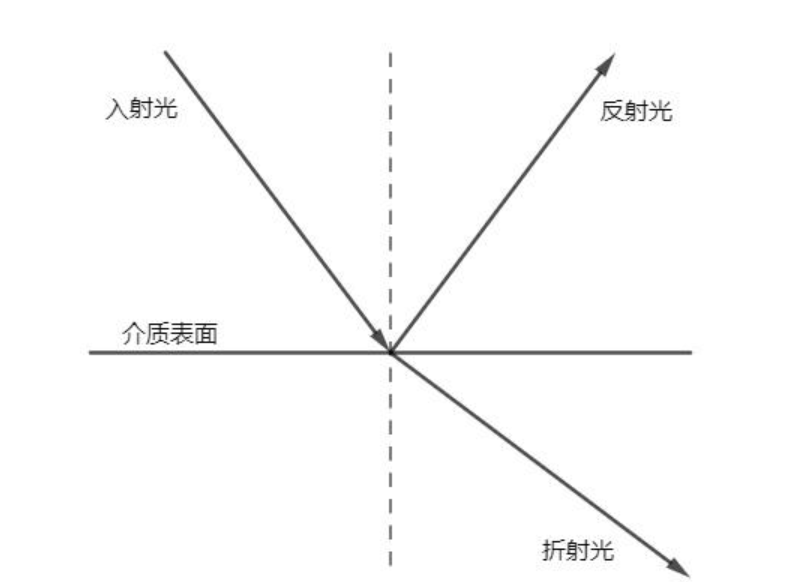
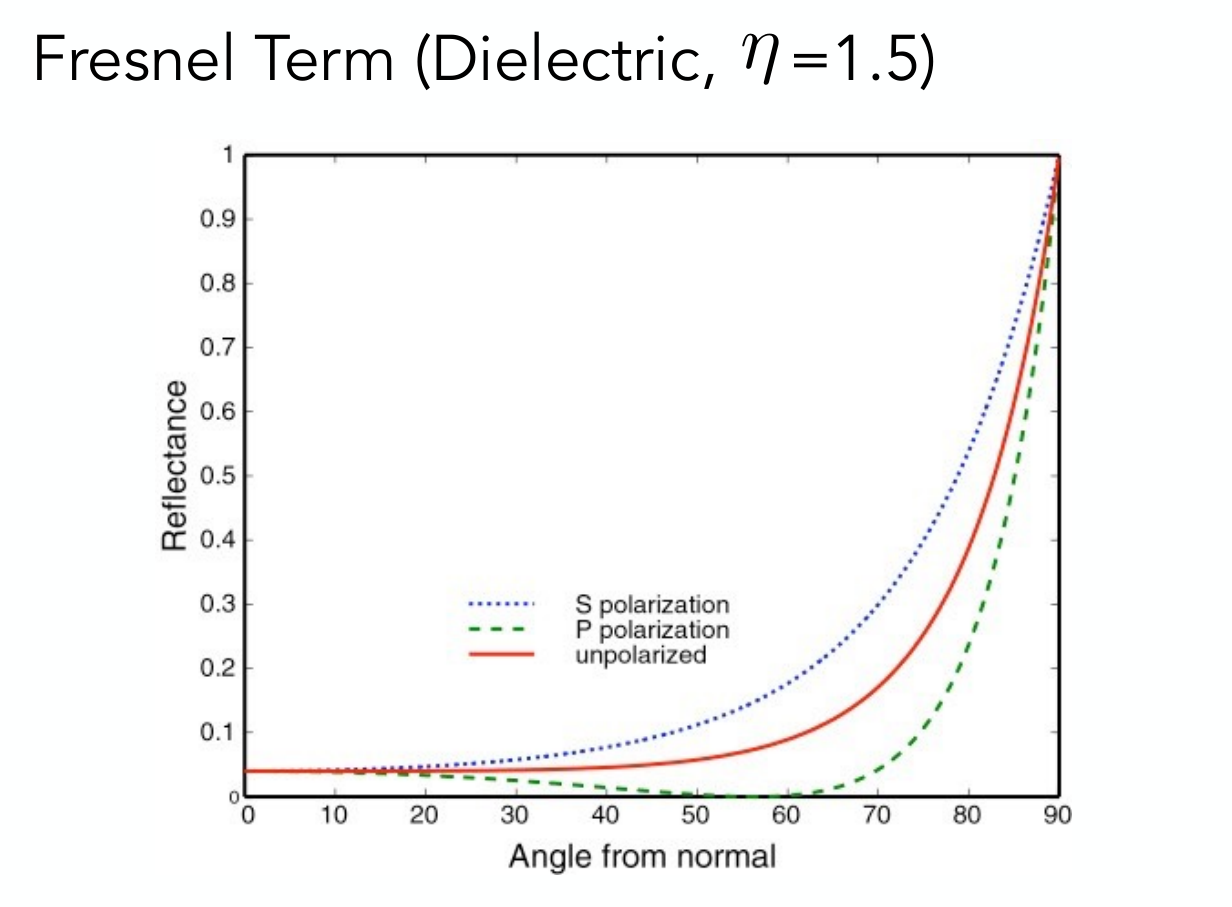
$F(\boldsymbol i, \boldsymbol h)$ aka Fresnel term决定不同入射角度时微表面模型的反射率.记入射光$\boldsymbol i$与微表面模型夹角为$\theta i$,折射光与法线家教为$\theta t$,则S波,P波的反射率分别为,
取二者的平均值, $$ R_{eff} = \frac{1}{2}(R_s + R_p) $$ 对于电介质,其反射率随观察角度和法线夹角$\theta$增大而增大.
note: Microfacet model的反射都视为镜面反射,因此给定入射方向wi与出射方向wo,半程向量h就视为法线方向。
用Schlick近似Fresnel term,
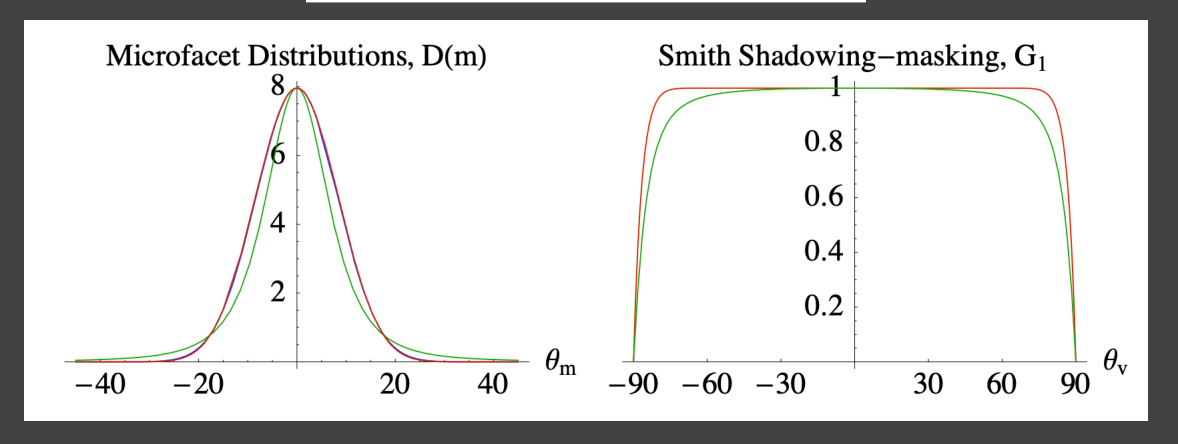
$D(\boldsymbol h)$ term aka Normal Distribution Function(NDF) 决定微表面法线的分布情况.GGX法线分布, $$ D_{GGX}(\boldsymbol h) = \frac{\alpha^2}{\pi ((\boldsymbol n, \boldsymbol h)^2\cdot(\alpha^2-1)+1)^2}\ \text{where } \alpha = roughness^2, \boldsymbol n \text{is the integral normal of the microfacet model.} $$ roughness越大,微表面模型越接近diffuse,roughness越小,越glossy
$Denote (n, h) = x$ ,对$x$求导,可以得到$D_{GGX}$随$x$增大而增大,即$\boldsymbol n$与$\boldsymbol h$夹角越小,$D_{GGX}$越大。
$G(\boldsymbol i, \boldsymbol o, \boldsymbol h)$ term aka Shadowing-Masking term(Geometry term).当入射光或者出射光方向近乎与法线垂直时(物体边缘),Microfacet BRDF的分母会趋近于0,导致物体边缘异常亮.
将G分为shadowing and masking两项, $$ G(\boldsymbol i, \boldsymbol o, \boldsymbol n) = G_1(\boldsymbol i, \boldsymbol n) G_1(\boldsymbol o, \boldsymbol n) $$ 如果把光线入射反向记作作$\boldsymbol i$,观察方向方向记$\boldsymbol o$,那么$G_1(\boldsymbol i, \boldsymbol h)$对应shadowing term,$G_1(\boldsymbol o, \boldsymbol h)$对应masking term.
$E_{\mu_0}$ 的推导
$E_{\mu}$ 因为要计算出射的总能量所以Fresnel term取1,代码是中是在半球上直接采样$w_i$,因此对应的积分用Monte-Carlo Integral表示为, $$ I = E(\frac{fr\cdot cos(\theta_i)}{pdf}) $$
反射的总能量为$E_{\mu_o}$,则损失的能量为$1-E_{\mu_o}$,考虑BRDF的对称性,改写为$c(1-E_{\mu_i})(1-E_{\mu_o})$,
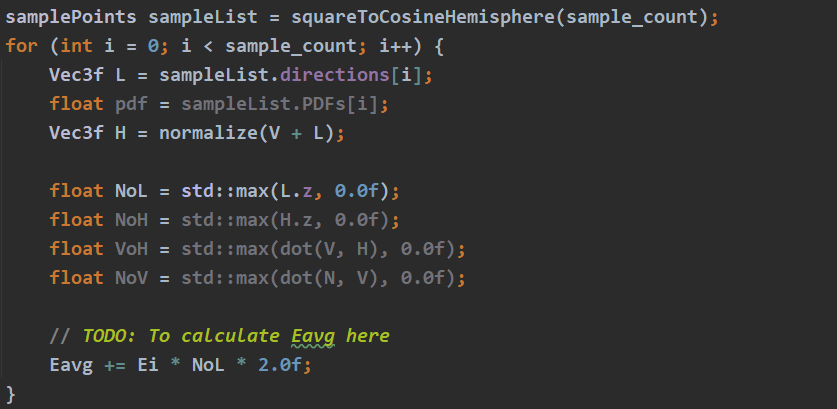
$E_{avg}$ 只是roughness的函数,不是出射方向V的函数,因此在IntegrateEmu中只要计算在该出射方向下的随机取样得到的函数均值,main函数中第二层循环遍历了$sin\theta$的值进行了黎曼和形式的积分.
TODO:
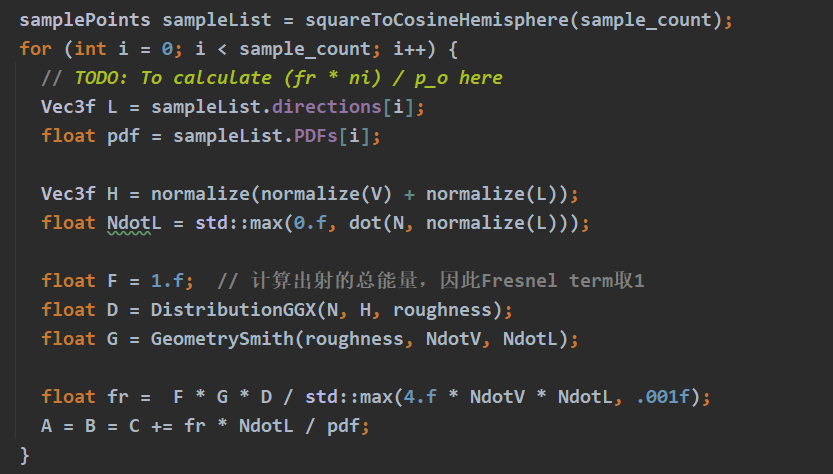
实现GGX,GeometrySmith与FresnelSchlick,直接照抄Emu_MC.cpp中的实现.
根据预计算的$E_{\mu}$与$E_{avg}$计算损失的能量对应的BDRF$f_{ms}$,对于有颜色的材质,会有自然存在的能量损失,因此在$f_{ms}$基础上再乘上一个系数$f_{add}$,最终的BRDF, $$ f_r = f_{micro} + f_{add} \cdot f_{ms} $$