A simplified version of the travelling salesman problem
- To gain further experience with Test-Driven-Development (TDD)
- Solving complex problems with programs
- Further practice using the Travis Continuous Integration (CI) process
Suppose there are a number of "cities", as in shown in Figure 1 below:
The distance between any two cities is the standard Euclidean distance, that is,
√((x1-x2)2+(y1-y2)2)
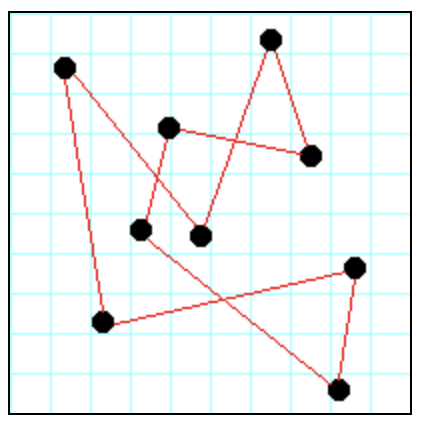
A traveling salesman wishes to visit every city exactly once, then return to their starting point. (It doesn't matter what city is the starting point.) Such a path is called a circuit, as in Figure 2 below:
However, the salesman also wishes to minimise the total distance that must be traveled.
This is a classic computer science problem, known as the Traveling Salesman problem.
Algorithms for finding reasonably good solutions are available on the web, however, I will use a hill climbing approach, where I start with "any" solution, and try to progressively improve it until I can't improve it any more.
The final solution is unlikely to be the optimal but that's okay, so long as it isn't obviously terrible.
city-data.txt, contains the latitudes and longitudes of the fifty state
capitals of the U.S.A.
Each line contains:
- the name of the state,
- the name of the city,
- the latitude, and
- the longitude.
This "road map" represents the path the salesman follows, starting with the first city in the list and ending back at the first city in the list.
The pytest unit testing framework is used to produce the solution to the
Travelling Salesman Problem using Test Driven Development