#Parallel Convex Hull Term Project A EE379K (Multicore Computing) term project written by Kapil Gowru (@kgowru), Mathew Kurian (@bluejamesbond), and Ankit Tandon (@ankittandon). The project tackles the objective of parallelizing three convex hull algorithms: Quickhull, Gift Wrapping, and Graham Scan.

##License All source code (except HeavySort) - Copyright Kapil Gowru, Mathew Kurian, and Ankit Tandon
HeavySort - Copyright Ross Anderson

##GUI

###Instructions When the project is run from main() you will see a GUI pop up with a blank space and options on the right. The options are listed below:

• Points: Define the number of points you want on your set. Remember to press populate once you change your points.
• Algorithm: Select any of the three algorithms (QuickHull, Gift Wrapping, and Graham Scan) explained below.
• Threads: Enter the number of threads you wish to employ to compute the algorithm.
• Time Delay: Set the time delay of the algorithm so as to see the computation in real time.
• Start Button: Starts the algorithm with options defined above.
• Populate Button: Populates the set of points on the area.

##Convex Hull A convex hull is defined by wikipedia as an

"envelope of a set X of points in the Euclidean plane or Euclidean space that holds the smallest convex set that contains X. For instance, when is X is a bounded subset of the plane, the convex hull may be visualized as the shape formed by a rubber band stretched around X."

Our objective was to take the following serial convex hull algorithms and parrallelize them so as to utilize multiple threads. Once that was done we compared the performance with various number of threads to test the optimization resulting from parallelizing the algorithms. The sections below offer a brief description of the algorithm, the steps taken to parallelize it, and the resulting performance benefits.

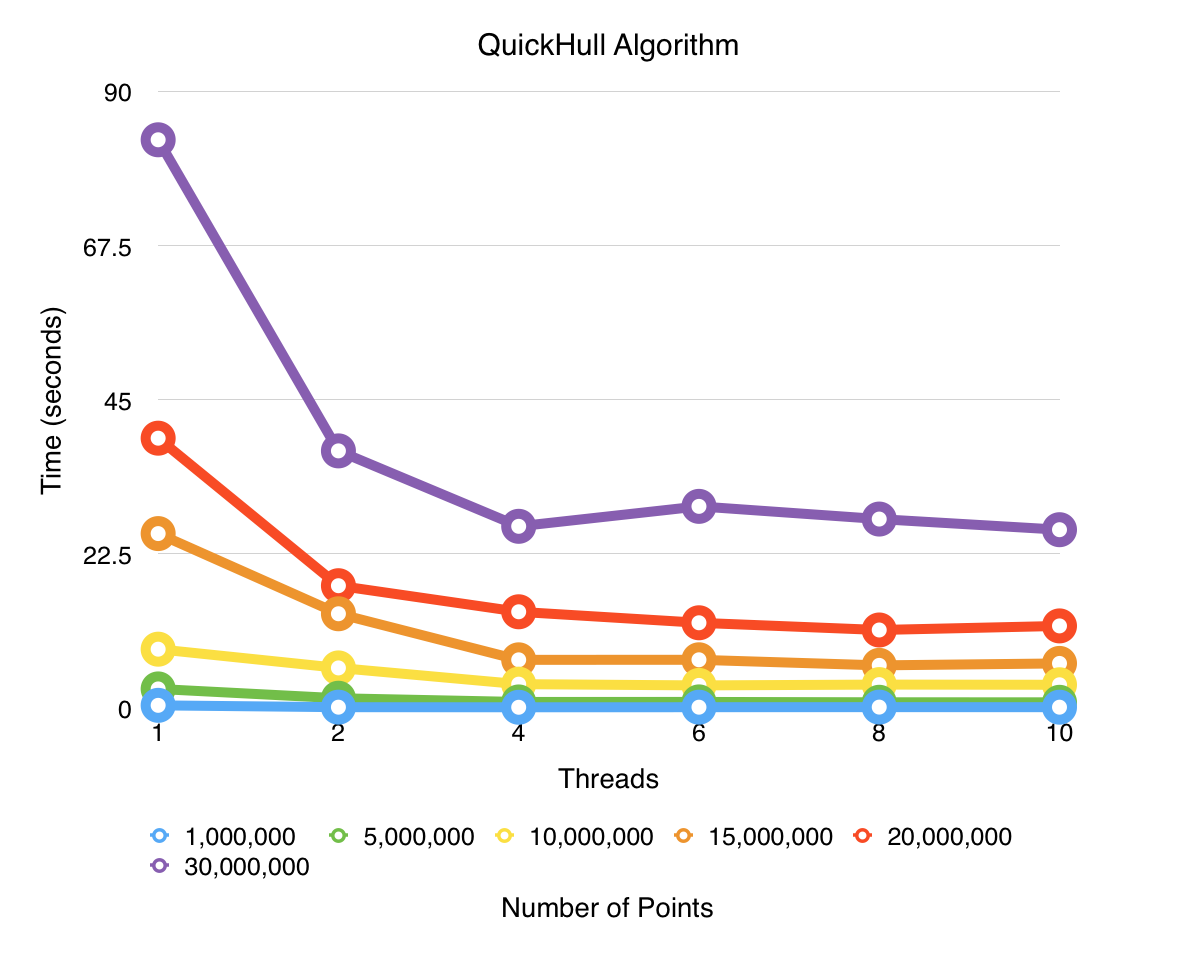
###QuickHull ####Algorithm Definition The quickhull algorithm for computing a convex hull utilizes a divide and conquer approach. The average complexity of this algorithm is O(n*log(n)) with the worst case run time of (On²). The basic pseudocode is as follows described on wikipedia:

1. Find two opposite coordinates in the set of point, S. (two opposite x or y coordinates). These two coordinates are defined to be on the convex hull by nature.
2. Split S into two subsets of points using the line formed by the two opposite coordinates.
3. Find a point on one side of the line that is the maximum distance from the line formed in the previous step. The two points found in the previous step in conjuction with the furthest point found in this step should form a triangle.
4. The points found inside this triangle are inherently not part of the convex hull, so they should be removed from the point set and ignored in the succeeding steps.
5. Repeat steps 3 and 4 on the two lines found in step 3 when forming a triangle.
6. Continue till all points have been removed, the resulting points constitute the convex hull

####Parallelizing Steps To parellize this algorithm we made the searching much more parallelized for each point. Additinally, added concurrency for each of the subsets and therefore signifcantly reduced calculations. Each subset produced k + 1 subsets which ultimately benifited from being parallelized.

####Graph

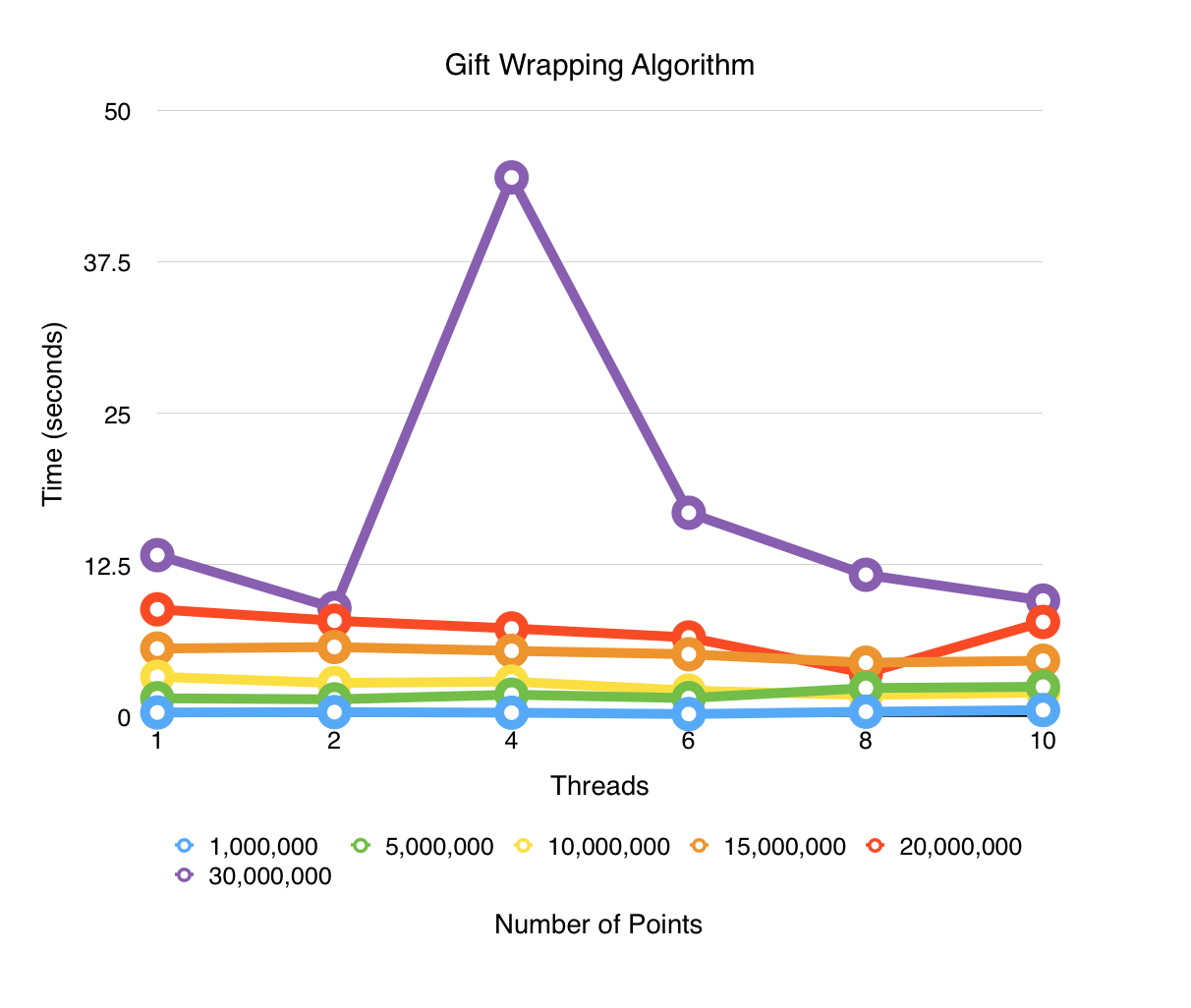
###Gift Wrapping ####Algorithm Definition The gift wrapping algorithm, also known as Jarvis march, is an algorithm defined by an O(nh) run time where n is the number of points and h is the number of points on the convex hull. The gift wrapping algorithm starts with a point, p, on the extrema of the set of points that is inherently on the convex hull. It then marches through the set of points to find the next point, q, that is most counterclockwise to p. Once q is found, p is set to q and proceeds to march through the points for the most counterclockwise. This continues till p reaches the origin of the convex hull or p[0]. The pseudo code taken from wikipedia is shown below:

1 jarvis(S)
2   pointOnHull = leftmost point in S
3   i = 0
4   repeat
5      P[i] = pointOnHull
6      endpoint = S[0]         // initial endpoint for a candidate edge on the hull
7      for j from 1 to |S|
8         if (endpoint == pointOnHull) or (S[j] is on left of line from P[i] to endpoint)
9            endpoint = S[j]   // found greater left turn, update endpoint
10      i = i+1
11      pointOnHull = endpoint
12   until endpoint == P[0]      // wrapped around to first hull point

####Parallelizing Steps To parallelize this algorithm, we utilized the t threads in two distinct ways. First, an n number of threads are given extrema's on the set of points. Extrema's are points on the north, east, south, and west most sides of the set of points. Once we find that are no more points that can be given to these wrap threads, we coin the remaining m threads as search threads. We then run the gift wrapping algorithm with each wrap thread. The search threads are then allotted to a specific wrap thread so as to optimize line 7-9 in the pseudocode in the previous section. The search threads terminate when they have completed searching through all of the set of points. The wrap threads terminate when they hit a point in their march that has already has been found to exist on the convex hull.

####Graph

###Graham Scan Serial ####Algorithm Definition The Graham scan is an algorithm very similar to the giftwrapping algorithm except that the points are sorted in polar order with relation to the lowest and farthest left point. This way as we iterate through points creating edges that create right turns, we do not need to visit every point. Graham Scan, as the name implies, scans points starting from the point that creates the most obtuse angle with the origin point. The runtime is O(nlogn) because of the sorting algorithms needed.

The pseudo code taken from wikipedia is shown below: First we define a counter-clockwise function that determines the orientation of 3 points with relation to each other.

# Three points are a counter-clockwise turn if ccw > 0, clockwise if
# ccw < 0, and collinear if ccw = 0 because ccw is a determinant that
# gives twice the signed  area of the triangle formed by p1, p2 and p3.
function ccw(p1, p2, p3):
    return (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x)

let N           = number of points
let points[N+1] = the array of points
swap points[1] with the point with the lowest y-coordinate
sort points by polar angle with points[1]

# We want points[0] to be a sentinel point that will stop the loop.
let points[0] = points[N]

# M will denote the number of points on the convex hull.
let M = 1
for i = 2 to N:
    # Find next valid point on convex hull.
    while ccw(points[M-1], points[M], points[i]) <= 0:
          if M > 1:
                  M -= 1
          # All points are collinear
          else if i == N:
                  break
          else
                  i += 1

    # Update M and swap points[i] to the correct place.
    M += 1
    swap points[M] with points[i]

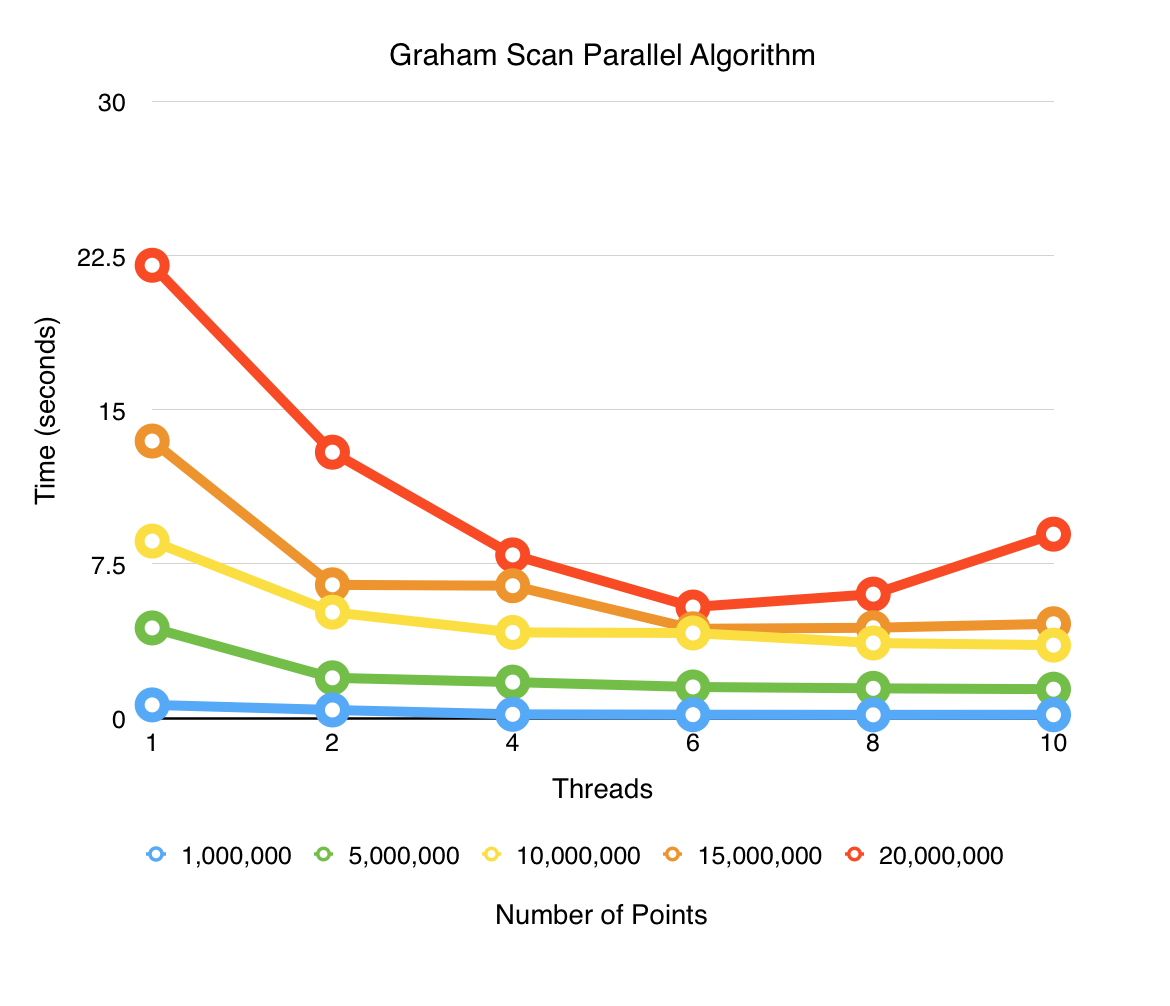
###Graham Scan Parallelized (Forced)

####Parallelizing Steps The Graham scan algorithm uses parallel HeavySort in order to optimize the sorting. Additional improvemets were made in the searching by breaking down the work into multiple threads. Unfortunately, the increased dependency between points on the convex hull made it virtually impossible to parallize even furthur. The biggest drawback with Graham scan is simply its depedency for loop.

####Graph

###Additional Experiments

• Optimal Count Thread Finder - a class to find the optimal threads to use for searching
• 3D QuickHull - ran out of time
• Statistical data for each algorithm