ship-trajectory-prediction

Note

This repository will soon be deprecated and no longer maintained. Updated links to the new repository will be provided shortly.

What the project does:

This repository hosts MATLAB files designed to carry out ship trajectory prediction on AIS data using Recurrent Neural Networks (RNNs).

The ship trajectory prediction model forms a core component of an operationally relevant (or "real-time") anomaly detection workflow, as part of the Nereus project.

Within the context of this anomaly detection workflow, the ship trajectory prediction model is designed to respond to anomalous events such as AIS "shut-off" events, signifying the absence of AIS transmissions for a predefined duration.

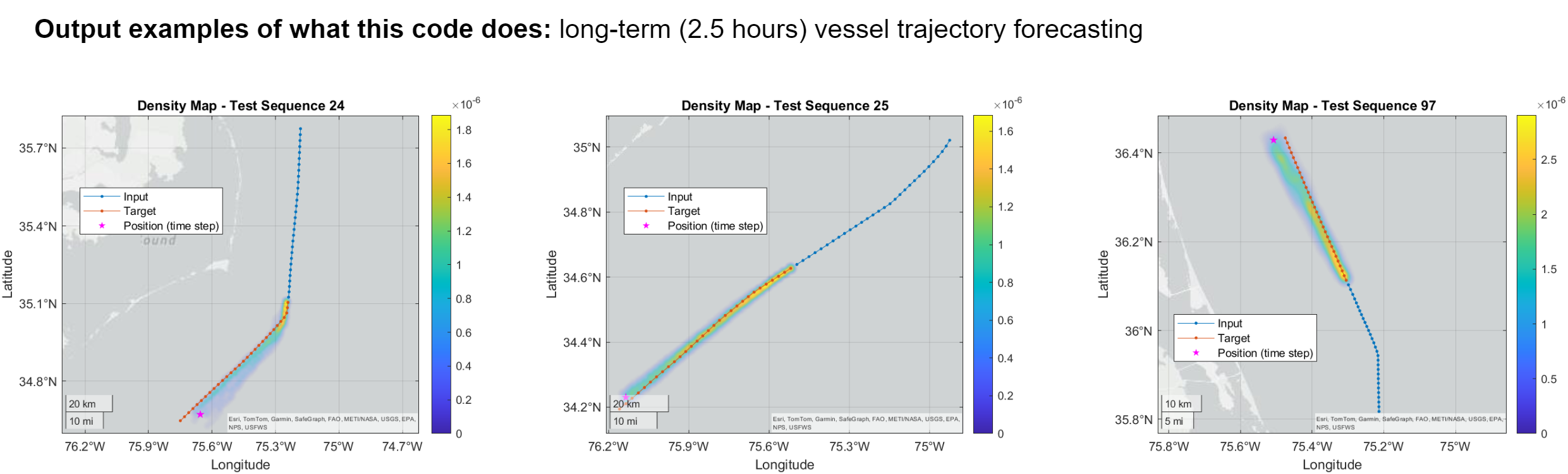
The model takes the ship's trajectory leading up to the "shut-off" event as input and generates a trajectory prediction for a user-defined period (e.g. 2.5 hours).

An assessment of the predicted trajectory is then conducted through a contextual analysis. If certain risk thresholds are exceeded, this triggers satellite "tip and cue" actions.

Note that this repository covers exclusively the ship trajectory prediction model and does not cover the other components of the anomaly detection workflow.

Why the project is useful:

The model's predictive capability enables the operational integration of ship observations from asynchronous self-reporting systems, like AIS, with imaging satellite technologies such as SAR and optical sensors, which require scheduling in advance.

In practical terms, if a target vessel is in motion, a trajectory prediction becomes essential for determining the acquisition area surrounding the likely position of the vessel when a satellite is scheduled to pass overhead.

The end goal is to enable end-users to efficiently identify anomalies demanding their attention amidst the (fortunately) abundant satellite data available to them, all within the constraints of their limited time and resources.

Getting started

Requirements

• MATLAB R2023b
• Deep Learning Toolbox
• Statistics and Machine Learning Toolbox
• Fuzzy Logic Toolbox
• Mapping Toolbox
• Parallel Computing Toolbox

Download or clone this repository to your machine and open it in MATLAB.

File description

Firstly, run the script s_data_preprocessing.m. This script performs the following data preprocessing steps:

1. Import data

2. Manage missing and invalid data

3. Aggregate data into sequences:

   • The data is aggregated into sequences or trajectories based on the Maritime Mobile Service Identity (MMSI) number, which uniquely identifies a vessel.
   • Simultaneously, the implied speed and implied bearing features are calculated based on the latitude and longitude data. This is because of the higher availability of latitude and longitude data as compared to the Speed Over Ground (SOG) and Course Over Ground (COG) data.
   • Next, the sequences are segmented into subsequences or subtrajectories using a predefined time interval threshold. In other words, if an AIS sequence has transmission gaps exceeding a specified time threshold, it is further split into smaller subsequences.

4. Resample subsequences:

   • The subsequences are resampled to regularly spaced time intervals by interpolating the data values.

5. Transform features:

   • A feature transformation is done to detrend the data (Chen et al., 2020). Specifically, the difference between consecutive observations is calculated for each feature. The transformed features are named similarly to the original ones, but with a delta symbol (Δ) or suffix "_diff" added to indicate the difference calculation, for example, the transformation of 'lat' (latitude) becomes 'Δlat' or 'lat_diff'.

6. Exclude empty and single-entry subsequences

7. Exclude outliers:

   • An unsupervised anomaly detection method is applied to the subsequences to detect and exclude outliers. Specifically, the isolation forest algorithm is used to detect and remove anomalies from the dataset. This step helps prevent outliers from distorting model training and testing.

8. Visualise subsequences

9. Apply sliding window:

   • A sliding window technique is applied to the subsequences, producing extra sequences from each one (these could be termed as "subsubsequences"). These generated sequences then serve as the input and response data for creating the model. Specifically, for each subsequence an input window and a response window of equal size are created. The windows are then progressively shifted by a specified time step. An illustrative example of this process is provided below:

     

10. Prepare training, validation and test data splits:

    • The input and response features are selected. Currently, lat_diff and lon_diff are selected from the available features.
    • The data is partitioned into training (80%), validation (10%) and test (10%) sets.
    • Additionally, the data is rescaled to the range [-1,1].

11. Save data variables

Secondly, run the script s_net_encoder_decoder.m which creates, trains and tests a recurrent sequence-to-sequence encoder-decoder model that incorporates both an attention mechanism and a Mixture Density Network (MDN) (Encoder-Decoder MDN). The network architecture is detailed in the Model details section.

A notable advantage of this model is its ability to capture uncertainty in the predictions, which is achieved through the incorporation of a Mixture Density Network (MDN).

MDNs combine traditional neural networks with a mixture model (commonly Gaussian Mixture Models, or GMMs) to predict a distribution over possible outcomes instead of a single point estimate.

MDNs are particularly suited for tasks like predicting ship trajectories where there may be multiple valid future paths that a ship could take under different conditions.

Specifically, this approach models the data as a mixture of multiple Gaussian distributions or components. It predicts the parameters for each of these components: the means (μ_i), standard deviations (σ_i) and the mixing coefficients (π_i), which indicate the weight or contribution of each Gaussian component in the mixture.

The output is a probability distribution that combines several Gaussian distributions. This allows the model to capture a wider range of possible outcomes and better express the uncertainty in scenarios where multiple future trajectories are possible.

(Note that the model is defined as a Model Function rather than a conventional MATLAB layer array, layerGraph or dlnetwork object. For details on their differences, refer to this documentation.)

Furthermore, the s_net_encoder_decoder.m script includes the following steps:

1. Load data
2. Preprocess data
3. Initialise model parameters
4. Define model function(s)
5. Define model loss function
6. Specify training options
7. Train model
8. Test model
9. Make example predictions

Tests

The unit and integration tests in tests/ as well as instructions on how to run them will be added in the near future.

Model details

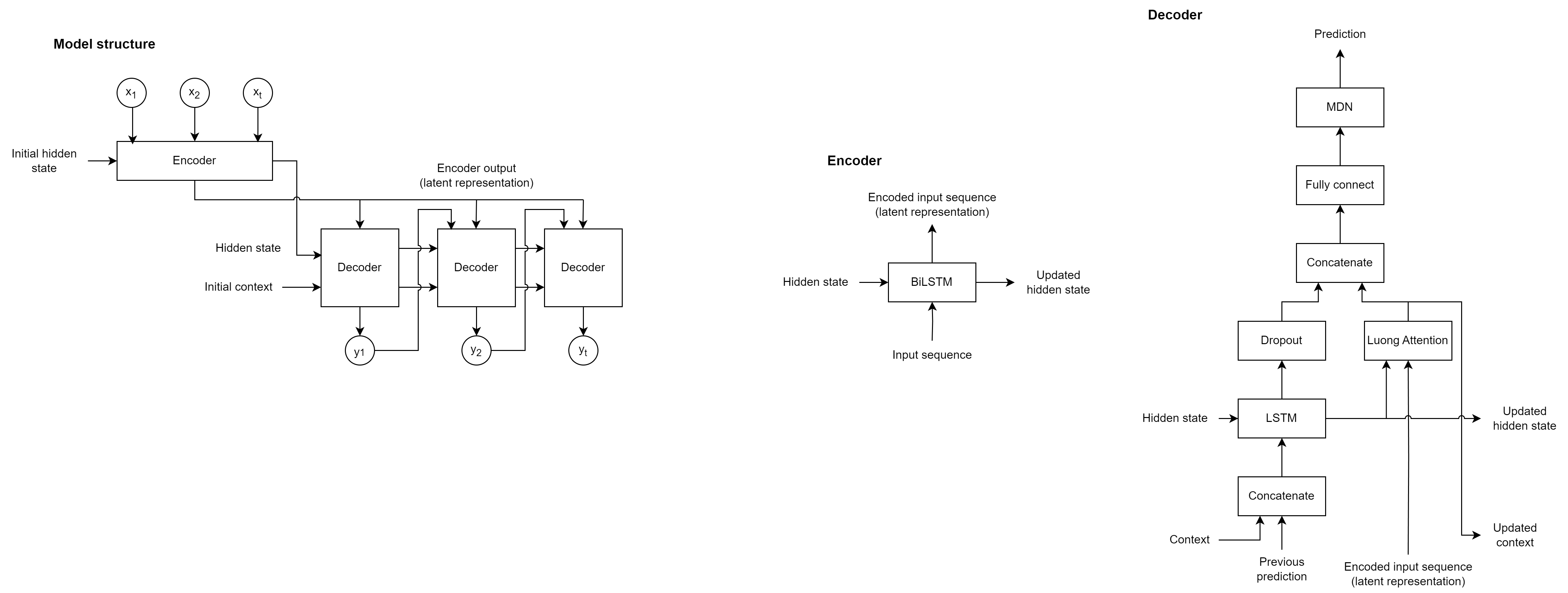
The recurrent sequence-to-sequence encoder-decoder model that incorporates both an attention mechanism and a Mixture Density Network (MDN) (Encoder-Decoder MDN) is shown in the diagram below:

The input sequence is represented as a sequence of points $x_1, x_2, \ldots, x_t$, where $x_i = (\Delta \text{lat}_i, \Delta \text{lon}_i)$ for $i = 1, 2, \ldots, t$. The same notation is used for the prediction sequence $y_1, y_2, \ldots, y_t$.

Moreover, the input sequence is passed through the encoder, which produces an encoded representation of the input sequence as well as a hidden state that is used to initialise the decoder's hidden state.

The encoder consists of a bidirectional LSTM (BiLSTM) layer. The decoder makes predictions at each time step, using the previous prediction as input (for inference), and outputs an updated hidden state and context values.

The decoder passes the input data concatenated with the input context through an LSTM layer, and takes the updated hidden state and the encoder output and passes it through an attention mechanism to determine the context vector.

The LSTM output follows a dropout layer before being concatenated with the context vector and passed through a fully connected layer.

The MDN layer of the decoder outputs the parameters of a mixture of Gaussians at each time step and output dimension.

Metrics and evaluation

The model is trained using the negative log-likelihood (NLL) loss, which is a measure of how well the MDN's predicted distribution matches the actual output or target data.

The training process randomly includes both scenarios where teacher forcing is used (i.e. the true target sequences are provided as inputs to the decoder at each time step) and where autoregressive decoding is required (i.e. the model uses its own predictions as inputs for subsequent time steps).

The model is then evaluated using the mean and max great circle distance between predicted and target sequences from the test set. Using the NLL loss during training and a physical distance (like the great circle distance) for evaluation combines the benefits of a robust training process with an evaluation metric that provides a direct real-world interpretation of the model’s performance.

For detailed results and associated data for each version of our project, please see the Releases page.

Limitations

Known limitations include:

• Sensitivity to the training dataset: The model's performance may be influenced by the composition and quality of the training data.
• Geographic and vessel type specificity: The model has been trained solely on cargo vessel types from a particular geographic region, which may restrict its generalisability to other vessel types and regions.

These limitations are acknowledged and should be taken into consideration when applying the model in different contexts.

References

MATLAB documentation:

• Custom Training Loops
• Train Deep Learning Model in MATLAB
• Define Custom Training Loops, Loss Functions, and Networks
• Sequence-to-Sequence Translation Using Attention

Journal articles:

• Capobianco et al., 2021.
• Chen et al., 2020.
• Sørensen et al., 2022.
• More to follow (including a literature review).

License

The license is available in the LICENSE file in this repository.