日本のリーチ麻雀のルールで、点数や期待値計算を行う C++ ライブラリです。
Miscellaneous programs about Japanese Mahjong
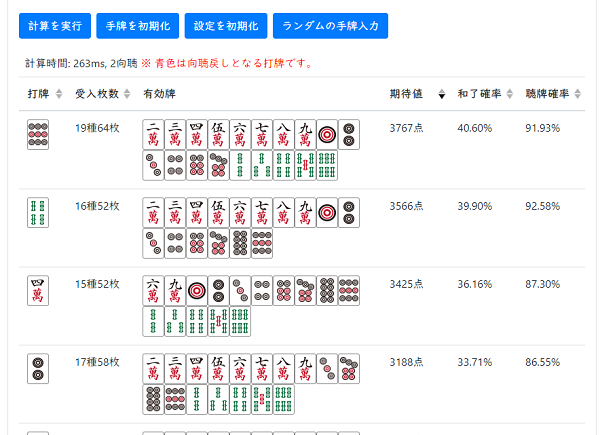
このライブラリを使った期待値計算機能を Web アプリにしたものを以下に公開しています。
- アプリの紹介: 麻雀 - 期待値計算ツール 何切るシミュレーター
- 期待値計算の詳細: 麻雀における期待値の計算方法
アルゴリズムに関しましては、以下のページを参考にさせていただいております。
- tomohxx. 麻雀アルゴリズム
- zurukumo. ネット上の向聴数計算アルゴリズムの知見に勝手に補足する
- KamichanR. 【麻雀】シャンテン数 高速計算アルゴリズム #C++ - Qiita
- Cryolite. A Fast and Space-Efficient Algorithm for Calculating Deficient Numbers (a.k.a. Shanten Numbers).pdf
- あら. あらの(一人)麻雀研究所
- Shanten Number Calculation (向聴数計算)
- Necessary Tile Calculation (有効牌計算)
- Unnecessary Tile Calculation (不要牌計算)
- Score Calculation (点数計算)
- Expected Score Calculation (聴牌確率/和了確率/期待値計算)
- English support
- C++17 (See C++ compiler support - cppreference.com)
- Boost C++ Libraries >= 1.66
- CMake >= 3.5
- CMake
- Visual Studio 2019 or 2022
Clone repogitory and build program.
git clone https://github.com/nekobean/mahjong-cpp.git
cd mahjong-cpp
mkdir build && cd build
# If you want the output to be in English, add the -DLANG_EN option (cmake .. -DLANG_EN)
cmake ..
make -j$(nproc)
make installRun sample program.
cd install/bin
sample_create_hand
sample_expected_score_calculation
sample_necessary_tile_calculation
sample_score_calculation
sample_shanten_number_calculation
sample_unnecessary_tile_calculationBuild and run container.
docker build . --tag mahjong-cpp
docker run -itP --name mahjong-cpp mahjong-cppBuild program on the created container.
git clone https://github.com/nekobean/mahjong-cpp.git
cd mahjong-cpp
mkdir build && cd build
cmake ..
make -j$(nproc)
make install- Syanten Number Calculation (向聴数計算)
- Score Calculation (点数計算)
- Necessary Tile Calculation (有効牌計算)
- Unnecessary Tile Selection (不要牌選択)
- Expected Score Calculation (期待値計算)
#include <iostream>
#include "mahjong/mahjong.hpp"
int main(int argc, char *argv[])
{
using namespace mahjong;
// Create hand by mpsz notation.
// 1m~9m: manzu, 0m: red5m
// 1p~9p: pinzu, 0p: red5p
// 1s~9s: souzu, 0s: red5s
// 1z=East, 2z=South, 3z=West, 4z=North, 5z=White, 6z=Green, 7z=Red
Hand hand1 = from_mpsz("222567345p333s22z");
// Convert hand to mpsz notation string by to_string().
std::cout << to_mpsz(hand1) << std::endl;
// Create hand by list of tiles.
Hand hand2 = from_array({Tile::Manzu2, Tile::Manzu2, Tile::Manzu2, Tile::Manzu5,
Tile::Manzu6, Tile::Manzu7, Tile::Pinzu3, Tile::Pinzu4,
Tile::Pinzu5, Tile::Souzu3, Tile::Souzu3, Tile::Souzu3,
Tile::South, Tile::South});
std::cout << to_mpsz(hand2) << std::endl;
// Create melds by specifying meld type and tiles.
// MeldType::Pong : pong (ポン)
// MeldType::Chow : chow (チー)
// MeldType::ClosedKong: closed kong (暗槓)
// MeldType::OpenKong : open kong (明槓)
// MeldType::AddedKong : added kong (加槓)
std::vector<Meld> melds = {
{MeldType::AddedKong, {Tile::East, Tile::East, Tile::East, Tile::East}},
{MeldType::Pong, {Tile::Manzu1, Tile::Manzu1, Tile::Manzu1}},
};
for (const auto &meld : melds) {
std::cout << to_string(meld) << " ";
}
std::cout << std::endl;
}#include <iostream>
#include "mahjong/mahjong.hpp"
int main(int argc, char *argv[])
{
using namespace mahjong;
// Create hand by mpsz notation or vector of tiles.
Hand hand = from_mpsz("222567m34p33667s");
// Hand hand = from_array({Tile::Manzu2, Tile::Manzu2, Tile::Manzu2, Tile::Manzu5,
// Tile::Manzu6, Tile::Manzu7, Tile::Pinzu3, Tile::Pinzu4,
// Tile::Souzu3, Tile::Souzu3, Tile::Souzu6, Tile::Souzu6,
// Tile::Souzu7});
// number of melds.
int num_melds = 0;
// Calculate minimum shanten number of regular hand, Seven Pairs and Thirteen Orphans.
auto [shanten_type, shanten] =
ShantenCalculator::calc(hand, num_melds, ShantenFlag::All);
std::cout << "shanten type: ";
for (int type : {ShantenFlag::Regular, ShantenFlag::SevenPairs,
ShantenFlag::ThirteenOrphans}) {
if (shanten_type & type) {
std::cout << ShantenFlag::Name.at(type) << " ";
}
}
std::cout << std::endl;
std::cout << "shanten: " << shanten << std::endl;
}#include <iostream>
#include "mahjong/mahjong.hpp"
int main(int argc, char *argv[])
{
using namespace mahjong;
// Create hand by mpsz notation or vector of tiles.
Hand hand = from_mpsz("222567m34p33667s");
// number of melds.
int num_melds = 0;
// Calculate necessary tiles.
auto [shanten_type, shanten, tiles] =
NecessaryTileCalculator::select(hand, num_melds, ShantenFlag::All);
std::cout << "shanten: " << shanten << std::endl;
for (auto tile : tiles) {
std::cout << Tile::Name.at(tile) + " ";
}
std::cout << std::endl;
}#include <iostream>
#include "mahjong/mahjong.hpp"
int main(int argc, char *argv[])
{
using namespace mahjong;
// Create hand by mpsz notation or vector of tiles.
Hand hand = from_mpsz("222567m34p33667s1z");
// number of melds.
int num_melds = 0;
// Calculate unnecessary tiles.
auto [shanten_type, shanten, tiles] =
UnnecessaryTileCalculator::select(hand, num_melds, ShantenFlag::All);
std::cout << "shanten: " << shanten << std::endl;
for (auto tile : tiles) {
std::cout << Tile::Name.at(tile) + " ";
}
std::cout << std::endl;
}
#include <iostream>
#include "mahjong/mahjong.hpp"
int main(int argc, char *argv[])
{
using namespace mahjong;
// Set round infomation.
/////////////////////////////////////////////////////
Round round;
round.rules = RuleFlag::RedDora | RuleFlag::OpenTanyao;
round.wind = Tile::East;
round.kyoku = 1;
round.honba = 0;
round.kyotaku = 1;
round.dora_indicators = {Tile::North};
round.uradora_indicators = {Tile::Pinzu9};
// If specifying dora, use set_dora().
// round.set_dora({Tile::East}), round.set_uradora({Tile::Pinzu1});
// Set player information
Hand hand = from_mpsz("222567345p333s22z");
Player player;
player.hand = hand;
player.melds = {};
player.wind = Tile::East;
const int win_tile = Tile::South;
const int flag = WinFlag::Tsumo | WinFlag::Riichi;
// Calculate score.
const Result result = ScoreCalculator::calc(round, player, win_tile, flag);
std::cout << to_string(result) << std::endl;
}[入力]
手牌: 222345567p333s22z
副露牌:
自風: 1z
自摸
[結果]
面子構成: [222p 暗刻子][345p 暗順子][567p 暗順子][333s 暗刻子][22z 暗対子]
待ち: 単騎待ち
役:
門前清自摸和 1翻
立直 1翻
40符2翻
和了者の獲得点数: 4900点, 子の支払い点数: 1300点
const auto [stats, searched] = ExpectedScoreCalculator::calc(config, round, player);=== Player ===
手牌: 026m1358p1345579s
副露牌:
自風: 1z
=== Necessary Tiles ===
2m type: 13, sum: 45, shanten: 3->3 tiles: 4m(4) 7m(4) 1p(3) 2p(4) 4p(4) 5p(3) 8p(3) 1s(3) 2s(4) 5s(2) 6s(4) 8s(4) 9s(3)
6m type: 25, sum: 86, shanten: 3->4 tiles: 1m(4) 2m(3) 3m(4) 4m(4) 5m(3) 6m(3) 7m(4) 1p(3) 2p(4) 3p(3) 4p(4) 5p(3) 6p(4) 7p(4) 8p(3) 9p(4) 1s(3) 2s(4) 3s(3) 4s(3) 5s(2) 6s(4) 7s(3) 8s(4) 9s(3)
1p type: 11, sum: 38, shanten: 3->3 tiles: 2m(3) 4m(4) 7m(4) 4p(4) 8p(3) 1s(3) 2s(4) 5s(2) 6s(4) 8s(4) 9s(3)
3p type: 23, sum: 80, shanten: 3->4 tiles: 1m(4) 2m(3) 3m(4) 4m(4) 7m(4) 1p(3) 2p(4) 3p(3) 4p(4) 5p(3) 6p(4) 7p(4) 8p(3) 9p(4) 1s(3) 2s(4) 3s(3) 4s(3) 5s(2) 6s(4) 7s(3) 8s(4) 9s(3)
5p type: 11, sum: 38, shanten: 3->3 tiles: 2m(3) 4m(4) 7m(4) 2p(4) 8p(3) 1s(3) 2s(4) 5s(2) 6s(4) 8s(4) 9s(3)
8p type: 13, sum: 45, shanten: 3->3 tiles: 2m(3) 4m(4) 7m(4) 1p(3) 2p(4) 4p(4) 5p(3) 1s(3) 2s(4) 5s(2) 6s(4) 8s(4) 9s(3)
1s type: 13, sum: 45, shanten: 3->3 tiles: 2m(3) 4m(4) 7m(4) 1p(3) 2p(4) 4p(4) 5p(3) 8p(3) 2s(4) 5s(2) 6s(4) 8s(4) 9s(3)
3s type: 22, sum: 77, shanten: 3->4 tiles: 1m(4) 2m(3) 3m(4) 4m(4) 7m(4) 1p(3) 2p(4) 3p(3) 4p(4) 5p(3) 6p(4) 7p(4) 8p(3) 9p(4) 1s(3) 2s(4) 3s(3) 4s(3) 5s(2) 6s(4) 8s(4) 9s(3)
4s type: 6, sum: 24, shanten: 3->3 tiles: 4m(4) 7m(4) 2p(4) 4p(4) 2s(4) 8s(4)
5s type: 10, sum: 35, shanten: 3->3 tiles: 2m(3) 4m(4) 7m(4) 1p(3) 2p(4) 4p(4) 5p(3) 8p(3) 1s(3) 8s(4)
7s type: 23, sum: 80, shanten: 3->4 tiles: 1m(4) 2m(3) 3m(4) 4m(4) 7m(4) 1p(3) 2p(4) 3p(3) 4p(4) 5p(3) 6p(4) 7p(4) 8p(3) 9p(4) 1s(3) 2s(4) 3s(3) 4s(3) 5s(2) 6s(4) 7s(3) 8s(4) 9s(3)
9s type: 10, sum: 35, shanten: 3->3 tiles: 2m(3) 4m(4) 7m(4) 1p(3) 2p(4) 4p(4) 5p(3) 8p(3) 1s(3) 6s(4)
0m type: 26, sum: 90, shanten: 3->4 tiles: 1m(4) 2m(3) 3m(4) 4m(4) 5m(3) 6m(3) 7m(4) 8m(4) 1p(3) 2p(4) 3p(3) 4p(4) 5p(3) 6p(4) 7p(4) 8p(3) 9p(4) 1s(3) 2s(4) 3s(3) 4s(3) 5s(2) 6s(4) 7s(3) 8s(4) 9s(3)
=== Tenpai Probability ===
turn 2m 6m 1p 3p 5p 8p 1s 3s 4s 5s 7s 9s 0m
1 77.78% 63.40% 73.33% 64.54% 72.73% 77.76% 77.70% 57.13% 63.05% 72.35% 65.84% 73.15% 61.26%
2 74.19% 59.09% 69.44% 60.15% 68.82% 74.17% 74.11% 52.42% 58.49% 68.41% 61.50% 69.26% 57.08%
3 70.15% 54.45% 65.12% 55.40% 64.48% 70.12% 70.07% 47.44% 53.59% 64.05% 56.77% 64.93% 52.58%
4 65.62% 49.46% 60.35% 50.29% 59.71% 65.59% 65.56% 42.23% 48.37% 59.25% 51.66% 60.15% 47.78%
5 60.59% 44.16% 55.14% 44.86% 54.50% 60.55% 60.54% 36.85% 42.87% 54.02% 46.21% 54.93% 42.68%
6 55.04% 38.59% 49.49% 39.14% 48.88% 55.00% 55.01% 31.38% 37.16% 48.38% 40.44% 49.28% 37.34%
7 48.98% 32.84% 43.45% 33.23% 42.88% 48.94% 48.97% 25.92% 31.34% 42.36% 34.46% 43.24% 31.82%
8 42.45% 27.02% 37.10% 27.26% 36.59% 42.41% 42.47% 20.60% 25.54% 36.07% 28.38% 36.88% 26.23%
9 35.55% 21.31% 30.55% 21.40% 30.10% 35.52% 35.59% 15.58% 19.93% 29.59% 22.38% 30.30% 20.72%
10 28.41% 15.85% 23.95% 15.84% 23.59% 28.40% 28.49% 11.04% 14.69% 23.09% 16.61% 23.69% 15.49%
11 21.28% 10.83% 17.52% 10.74% 17.25% 21.29% 21.39% 7.15% 10.03% 16.78% 11.30% 17.25% 10.68%
12 14.49% 6.50% 11.57% 6.37% 11.39% 14.52% 14.61% 4.04% 6.13% 10.98% 6.73% 11.31% 6.49%
13 8.50% 3.12% 6.49% 3.01% 6.40% 8.53% 8.60% 1.81% 3.17% 6.08% 3.19% 6.25% 3.18%
14 3.86% 0.93% 2.72% 0.87% 2.69% 3.87% 3.90% 0.49% 1.23% 2.49% 0.93% 2.55% 0.98%
15 1.00% 0.00% 0.59% 0.00% 0.59% 1.00% 1.00% 0.00% 0.26% 0.51% 0.00% 0.51% 0.00%
16 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00%
17 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00%
18 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00%
=== Win Probability ===
turn 2m 6m 1p 3p 5p 8p 1s 3s 4s 5s 7s 9s 0m
1 20.98% 13.34% 18.74% 14.83% 18.11% 20.90% 21.03% 12.00% 13.59% 18.11% 15.39% 18.92% 12.37%
2 18.24% 11.26% 16.15% 12.54% 15.60% 18.17% 18.30% 9.99% 11.45% 15.58% 13.05% 16.30% 10.46%
3 15.60% 9.31% 13.67% 10.39% 13.20% 15.54% 15.65% 8.13% 9.45% 13.16% 10.84% 13.80% 8.68%
4 13.07% 7.52% 11.33% 8.41% 10.94% 13.03% 13.12% 6.45% 7.62% 10.88% 8.79% 11.43% 7.03%
5 10.70% 5.90% 9.16% 6.60% 8.84% 10.66% 10.74% 4.96% 5.97% 8.76% 6.93% 9.23% 5.54%
6 8.50% 4.47% 7.18% 5.01% 6.93% 8.47% 8.54% 3.67% 4.51% 6.84% 5.27% 7.23% 4.21%
7 6.51% 3.24% 5.43% 3.63% 5.24% 6.49% 6.55% 2.59% 3.27% 5.14% 3.84% 5.45% 3.07%
8 4.76% 2.22% 3.91% 2.50% 3.77% 4.76% 4.80% 1.72% 2.25% 3.68% 2.65% 3.91% 2.12%
9 3.28% 1.42% 2.64% 1.60% 2.55% 3.28% 3.31% 1.06% 1.44% 2.48% 1.70% 2.63% 1.37%
10 2.09% 0.82% 1.64% 0.92% 1.59% 2.09% 2.11% 0.59% 0.84% 1.53% 0.98% 1.62% 0.80%
11 1.19% 0.41% 0.90% 0.45% 0.88% 1.19% 1.20% 0.28% 0.44% 0.83% 0.49% 0.88% 0.40%
12 0.57% 0.16% 0.41% 0.17% 0.40% 0.57% 0.58% 0.10% 0.19% 0.37% 0.19% 0.40% 0.16%
13 0.21% 0.04% 0.14% 0.04% 0.14% 0.21% 0.21% 0.02% 0.06% 0.12% 0.04% 0.13% 0.04%
14 0.04% 0.00% 0.02% 0.00% 0.02% 0.04% 0.04% 0.00% 0.01% 0.02% 0.00% 0.02% 0.00%
15 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00%
16 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00%
17 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00%
18 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00% 0.00%
=== Expected Score ===
turn 2m 6m 1p 3p 5p 8p 1s 3s 4s 5s 7s 9s 0m
1 1977.33 1100.60 1879.30 1423.04 1563.48 1962.67 2012.92 1030.85 1147.32 1527.20 1439.02 1876.73 657.61
2 1708.40 914.72 1611.65 1197.01 1336.88 1695.64 1740.36 852.95 959.71 1305.29 1214.49 1609.69 548.25
3 1450.86 744.79 1357.37 986.44 1122.43 1439.93 1479.08 690.49 786.63 1095.18 1004.38 1355.79 448.35
4 1207.23 591.96 1118.95 793.45 922.10 1198.08 1231.68 544.52 629.35 898.92 810.67 1117.48 358.43
5 980.21 456.97 899.04 619.63 738.09 972.76 1000.88 416.06 489.18 718.58 635.48 897.46 278.62
6 772.55 340.53 700.34 466.90 572.51 766.77 789.49 305.84 367.10 556.24 480.71 698.46 209.28
7 586.71 242.92 524.82 336.44 427.10 582.53 600.37 214.37 263.73 413.78 347.79 522.58 150.57
8 425.13 163.65 374.39 228.93 303.42 422.42 435.69 141.37 179.40 292.77 237.79 371.89 102.52
9 289.94 102.20 250.62 144.54 202.49 288.36 297.56 86.14 113.80 194.24 151.08 247.97 64.94
10 182.30 57.47 154.10 82.53 124.12 181.51 187.38 47.12 65.74 118.14 86.86 151.62 37.22
11 102.21 27.78 83.93 40.54 67.36 101.89 105.33 22.06 33.31 63.55 42.82 81.90 18.45
12 48.20 10.49 37.95 15.45 30.37 48.11 49.80 7.98 13.90 28.20 16.39 36.50 7.17
13 17.01 2.38 12.46 3.50 9.97 17.00 17.60 1.70 4.19 8.95 3.73 11.62 1.68
14 3.29 0.00 2.04 0.00 1.66 3.29 3.40 0.00 0.65 1.35 0.00 1.73 0.00
15 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
16 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
17 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
18 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00