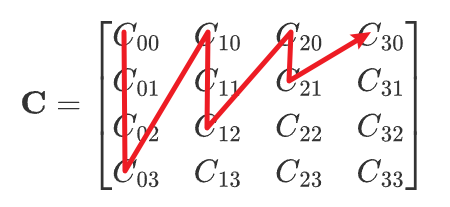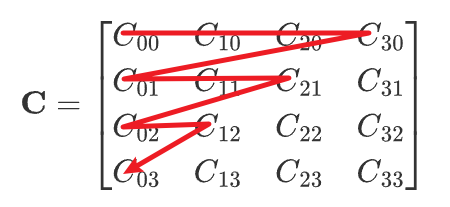N-order polynomial surface fitting with Eigen (Least squares).
git clone -b main --recursive https://github.com/nescirem/SurfacePolynomialFitting.git
cd SurfacePolynomialFitting
mkdir build && cd build
cmake ..
make
Execute./SPF ${N},N can be any natural number.
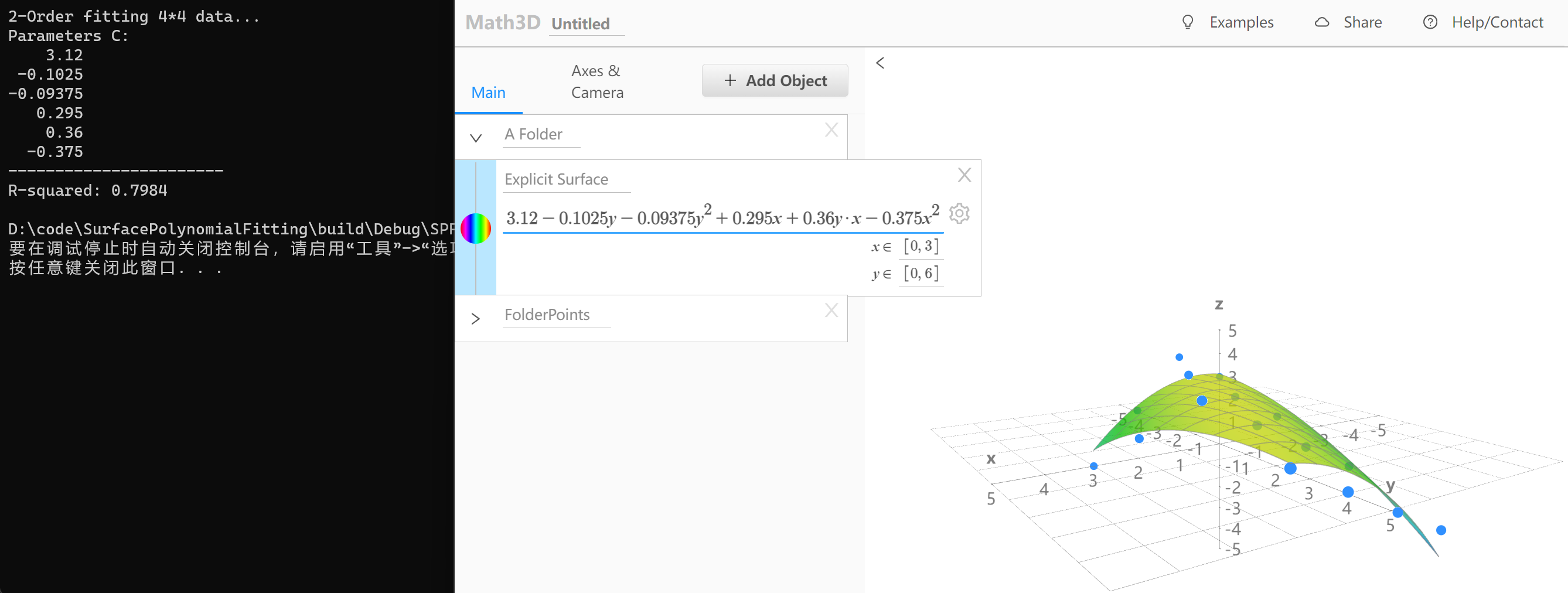
- N=2
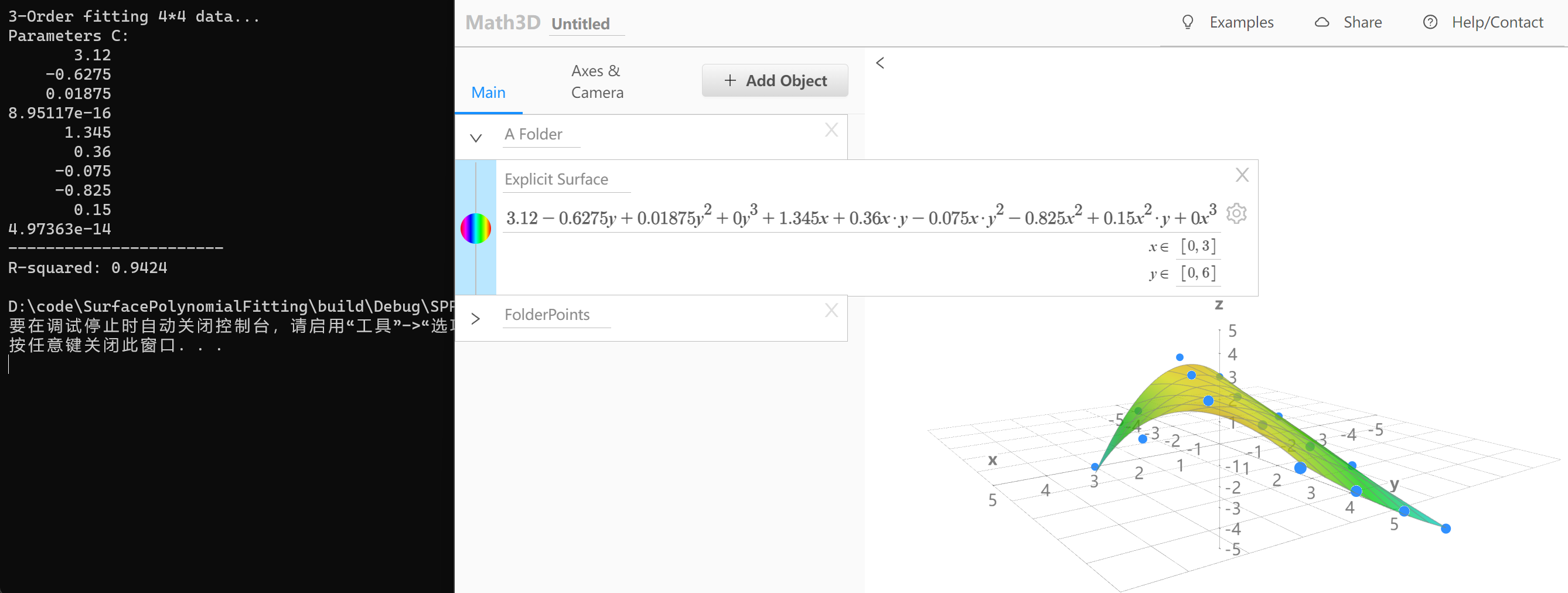
- N=3
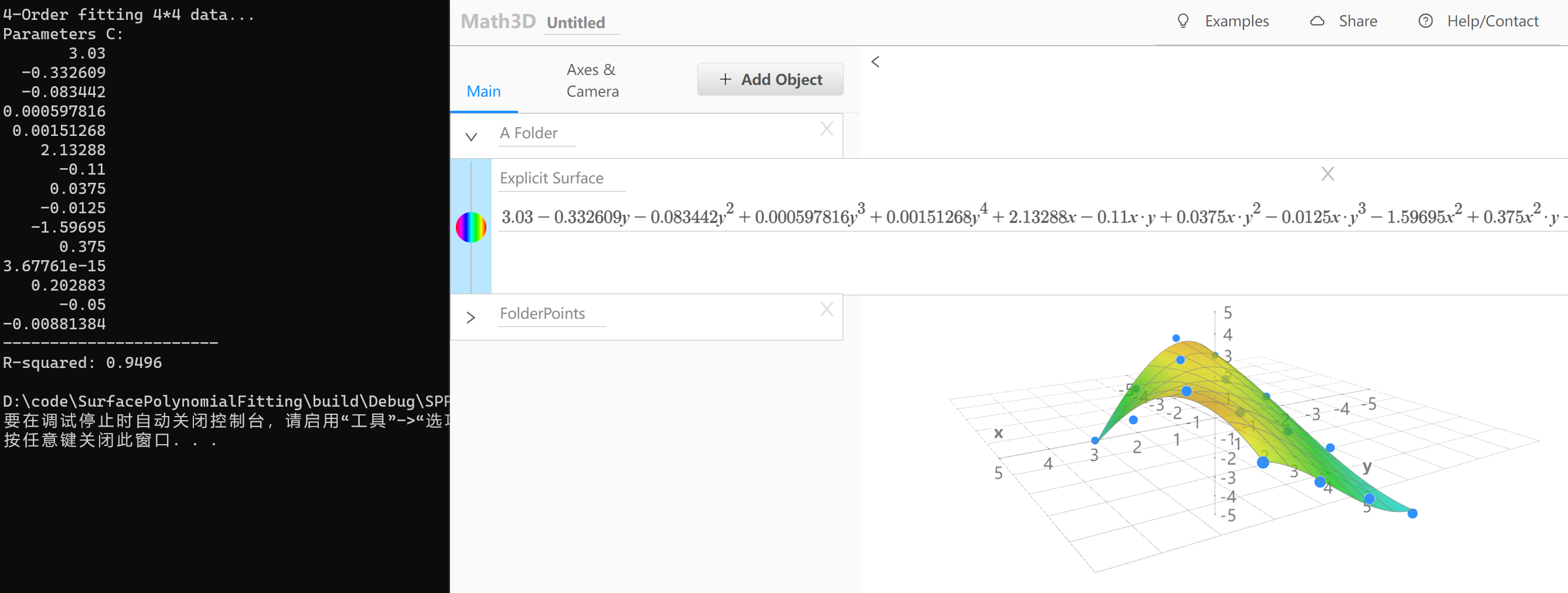
- N=4
A detailed explanation of the least squares fitting of a two-variable N-order orthogonal polynomial for a dataset with
The sum of the squared errors for each data point within the dataset is:
The least squares method considers that the optimal coefficients
The
The
U can change this order as:
by change that code:
//X(k, index++) = std::pow(x, i) * std::pow(y, j); // C_{00},C{01},...
X(k, index++) = std::pow(x, j) * std::pow(y, i); // C_{00},C_{10},...That's all.