Recursividade (em desenvolvimento)

📚 Minha visão sobre a técnica de recursividade na progamação

Minha Definição:

Uma função recursiva é uma função que chama a si própia 🤝

tipos de recursividade:

A função recursiva pode se auto chamar dentro do própio escopo. Esse tipo de método é chamado de Recursividade direta. utilizando o exemplo de cálculo de fatorial, é possivel ver a recursividade direta na seguinte função:

  def fatorial(n):
    if n <= 1:
      return 1
    else:
      return n * fatorial(n-1)

codigo 1

Note que na estrutura de condição else da função fatorial é passada a própia função.

O outro tipo de função recursiva é a recursividade indireta, onde, a função recursiva é chamada a partir de outra função. Exemplo:

def exibir_fatorial(num):
  print(fatorial(num))

codigo 2

A função exibir_fatorial exibe na tela o resultado da função recursiva fatorial.

Como a recursividade funciona?

Primeiro é necessario saber que a recursividade faz a divisão do problema em duas partes:

O caso base que é uma forma do problema que se da uma resposta direta.

def fatorial(n):
  #caso base
  if n<= 1:
    return 1

O caso geral que seria um caso mais completo, no entanto, não é a solução final.

#caso base
if n<= 1:
  return 1
#recursao esta aqui:
else:
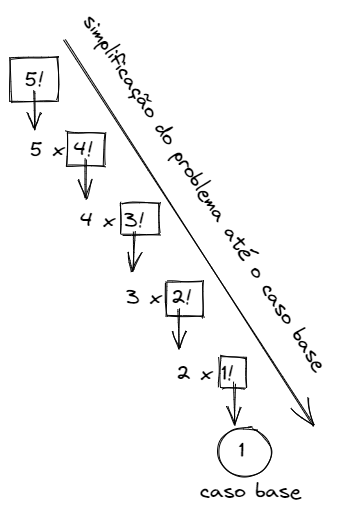
  return n * fatorial(n-1)

Considerando a lógica da definição do cálculo de fatórial, é possivel encontrar o caso base, os resultados de 1! e 0! que são iguais a 1. Sabendo disso, a função recursiva irá simplificar o cálculo do fatorial como se fosse uma estrutura de repetição. Irá chamar a si própia até simplificar o suficiente para chegar ao caso base. Observe a imagem:

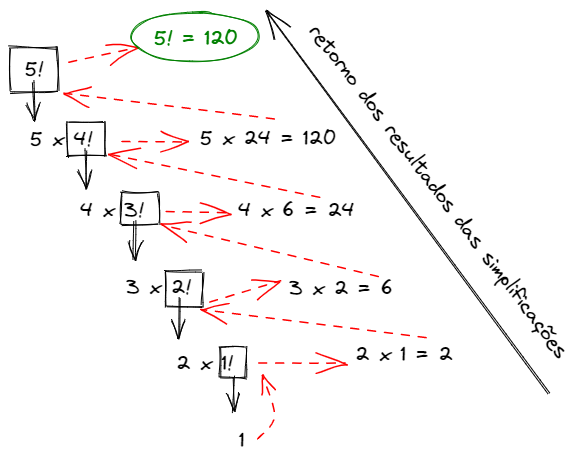
Após chegar ao caso base, a função recursiva irá resolver os casos intermediários ate obter o resultado completo. Confira a imagem:

Porque usar a recursividade ?

Como dito anteriormente, a recursividade funciona como se fosse uma estrutura de repetição. Há casos onde a solução iterativa é difícil de se obter ou tem desempenho inferior à recursiva, nestes casos utiliza-se a recursividade. No entanto, sempre que possível deve-se optar por uma solução não recursiva, visto que, a recursividade abre mão do desempenho devido as 'N' chamadas de si própia, assim, gastando mais processamento e quantidade de memória principal.

Algumas vezes a implementação recursiva pode ser "convertida" em iterativa. Veja esse exemplo da utilização da estrutura de repetição while na resolução do mesmo problema:

def fatorial(n):
    fatorial = 1
    i=n
    while(i>0):
        fatorial*=i
        i=i-1
    return fatorial


numero = int(input("digite um numero para saber seu fatorial: "))
print(fatorial(numero))

Muita das vezes a otimização de códigos é feita diminuindo a complexidade de seus algoritimos, neste caso, a estrutura de repetição substitui a recursão para que haja mais perfomance de processamento e memória.

Testes de performance:

É possivel verificar o script de teste clicando aqui.

nos testes foi utilizado o tempo de execução de cada