Merge pull request wangzheng0822#201 from Liam0205/notes

[notes][20_hashtable] done.

notes/18_hashtable/readme.md

@@ -1,69 +1,69 @@
-# 散列表
-
-散列表是数组的一种扩展，利用数组下标的随机访问特性。
-
-## 散列思想
-
-* 键/关键字/Key：用来标识一个数据
-* 散列函数/哈希函数/Hash：将 Key 映射到数组下标的函数
-* 散列值/哈希值：Key 经过散列函数得到的数值
-
-![](https://static001.geekbang.org/resource/image/92/73/92c89a57e21f49d2f14f4424343a2773.jpg)
-
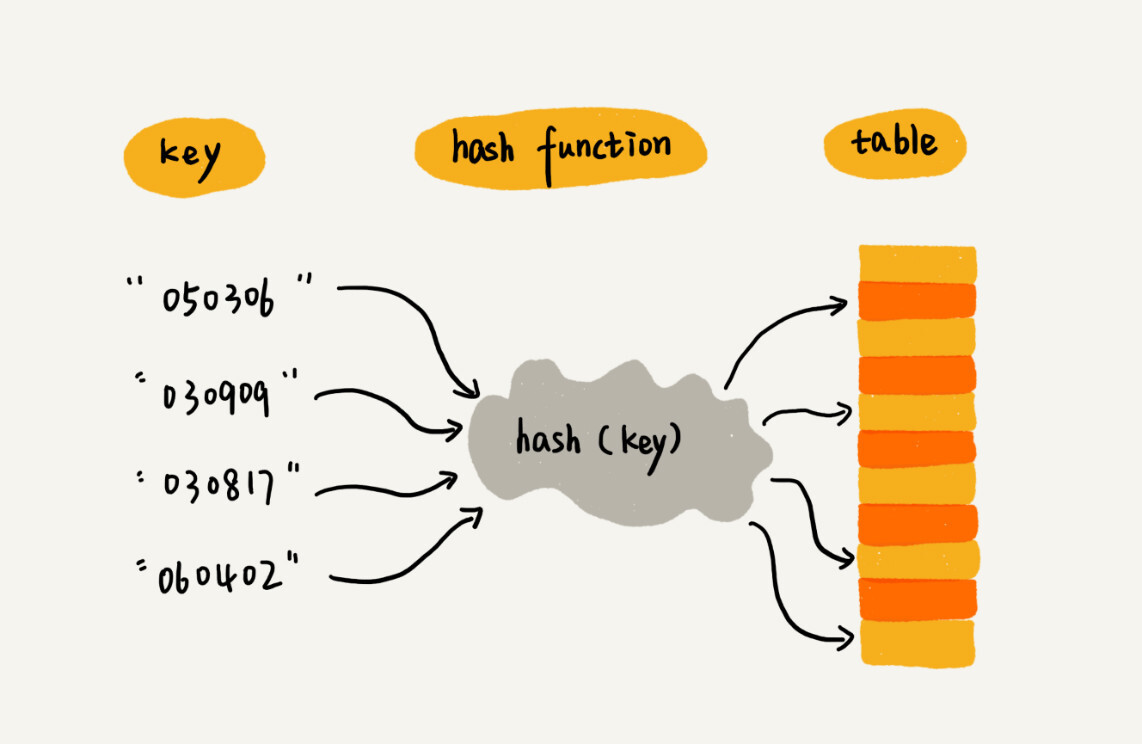-本质：利用散列函数将关键字映射到数组下标，而后利用数组随机访问时间复杂度为 $\Theta(1)$ 的特性快速访问。
-
-## 散列函数
-
-* 形式：`hash(key)`
-* 基本要求
-  1. 散列值是非负整数
-  1. 如果 `key1 == key2`，那么 `hash(key1) == hash(key2)`
-  1. 如果 `key1 != key2`，那么 `hash(key1) != hash(key2)`
-
-第 3 个要求，实际上不可能对任意的 `key1` 和 `key2` 都成立。因为通常散列函数的输出范围有限而输入范围无限。
-
-## 散列冲突¡
-
-* 散列冲突：`key1 != key2` 但 `hash(key1) == hash(key2)`
-
-散列冲突会导致不同键值映射到散列表的同一个位置。为此，我们需要解决散列冲突带来的问题。
-
-### 开放寻址法
-
-如果遇到冲突，那就继续寻找下一个空闲的槽位。
-
-#### 线性探测
-
-插入时，如果遇到冲突，那就依次往下寻找下一个空闲的槽位。（橙色表示已被占用的槽位，黄色表示空闲槽位）
-
-![](https://static001.geekbang.org/resource/image/5c/d5/5c31a3127cbc00f0c63409bbe1fbd0d5.jpg)
-
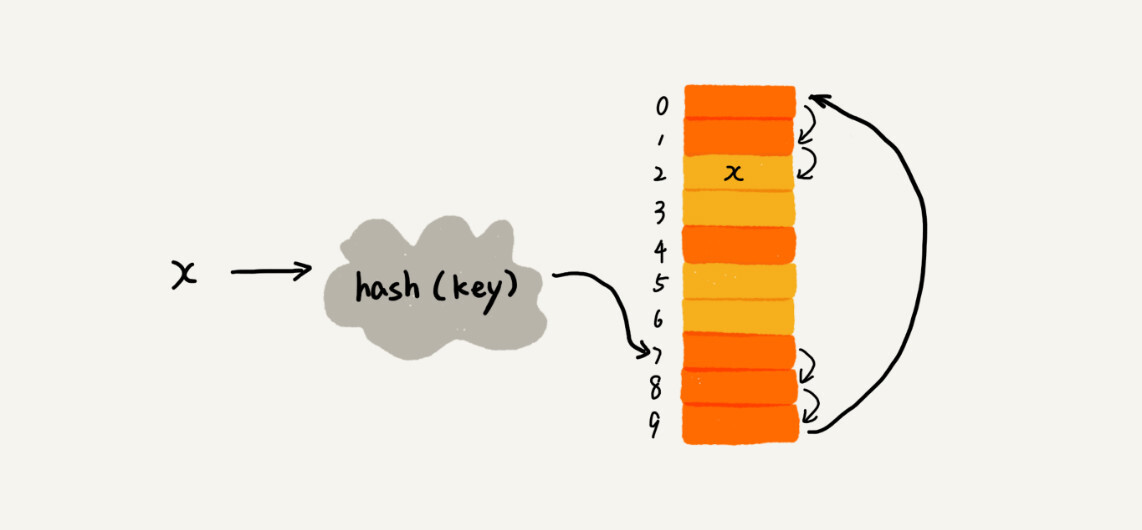-查找时，如果目标槽位上不是目标数据，则依次往下寻找；直至遇见目标数据或空槽位。
-
-![](https://static001.geekbang.org/resource/image/91/ff/9126b0d33476777e7371b96e676e90ff.jpg)
-
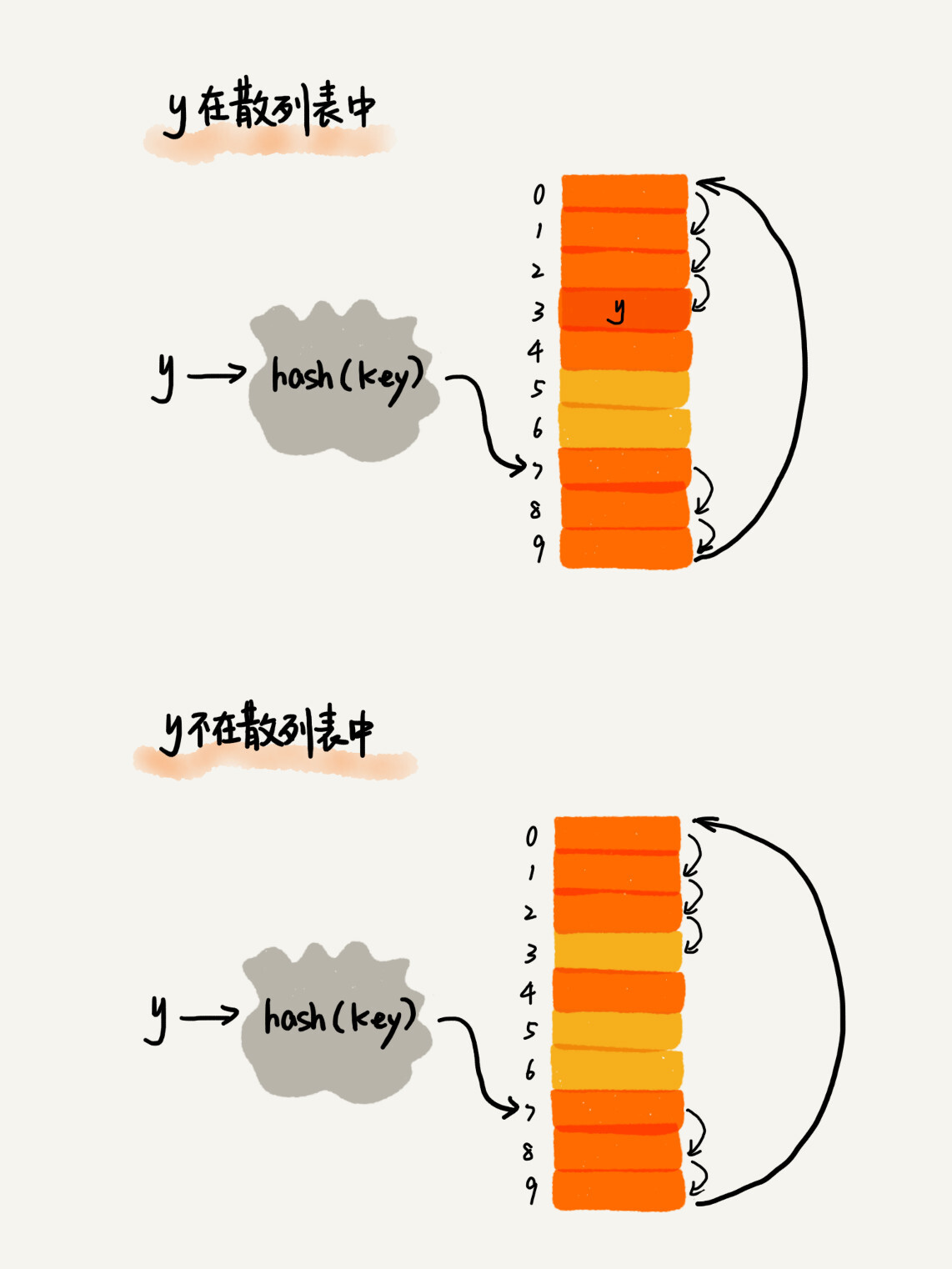-删除时，标记为 `deleted`，而不是直接删除。
-
-#### 平方探测（Quadratic probing）
-
-插入时，如果遇到冲突，那就往后寻找下一个空闲的槽位，其步长为 $1^2$, $2^2$, $3^2$, $\ldots$。
-
-查找时，如果目标槽位上不是目标数据，则依次往下寻找，其步长为 $1^2$, $2^2$, $3^2$, $\ldots$；直至遇见目标数据或空槽位。
-
-删除时，标记为 `deleted`，而不是直接删除。
-
-#### 装载因子（load factor）
-
-$\text{load factor} = \frac{size()}{capacity()}$
-
-### 链表法
-
-所有散列值相同的 key 以链表的形式存储在同一个槽位中。
-
-![](https://static001.geekbang.org/resource/image/a4/7f/a4b77d593e4cb76acb2b0689294ec17f.jpg)
-
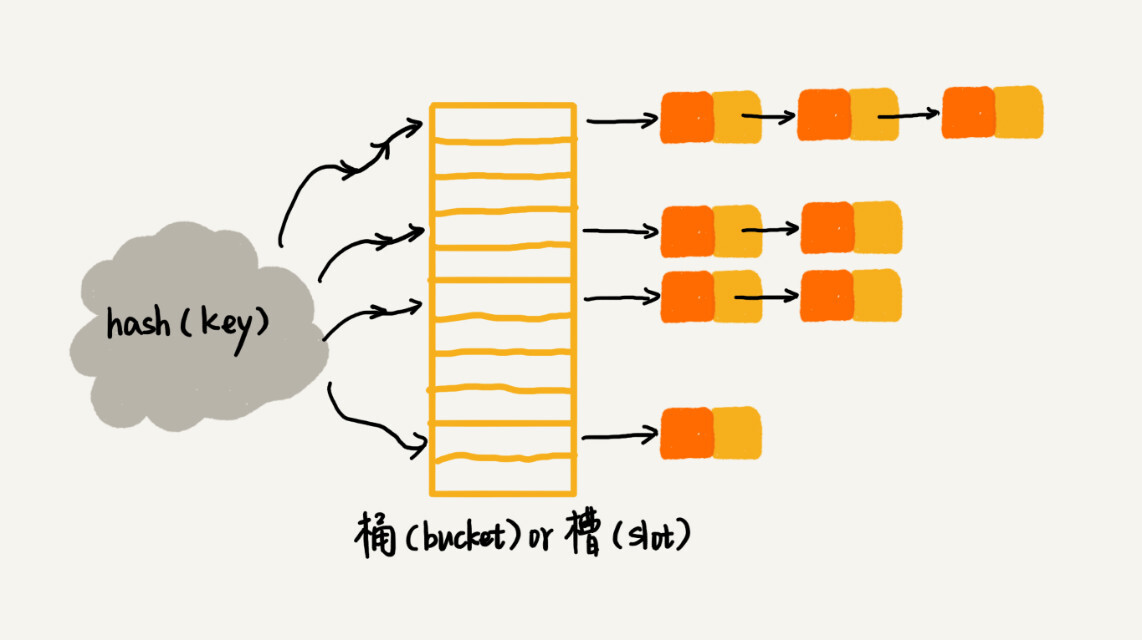-插入时，不论是否有冲突，直接插入目标位置的链表。
-
-查找时，遍历目标位置的链表来查询。
-
-删除时，遍历目标位置的链表来删除。
+# 散列表
+
+散列表是数组的一种扩展，利用数组下标的随机访问特性。
+
+## 散列思想
+
+* 键/关键字/Key：用来标识一个数据
+* 散列函数/哈希函数/Hash：将 Key 映射到数组下标的函数
+* 散列值/哈希值：Key 经过散列函数得到的数值
+
+![](https://static001.geekbang.org/resource/image/92/73/92c89a57e21f49d2f14f4424343a2773.jpg)
+
+本质：利用散列函数将关键字映射到数组下标，而后利用数组随机访问时间复杂度为 $\Theta(1)$ 的特性快速访问。
+
+## 散列函数
+
+* 形式：`hash(key)`
+* 基本要求
+  1. 散列值是非负整数
+  1. 如果 `key1 == key2`，那么 `hash(key1) == hash(key2)`
+  1. 如果 `key1 != key2`，那么 `hash(key1) != hash(key2)`
+
+第 3 个要求，实际上不可能对任意的 `key1` 和 `key2` 都成立。因为通常散列函数的输出范围有限而输入范围无限。
+
+## 散列冲突
+
+* 散列冲突：`key1 != key2` 但 `hash(key1) == hash(key2)`
+
+散列冲突会导致不同键值映射到散列表的同一个位置。为此，我们需要解决散列冲突带来的问题。
+
+### 开放寻址法
+
+如果遇到冲突，那就继续寻找下一个空闲的槽位。
+
+#### 线性探测
+
+插入时，如果遇到冲突，那就依次往下寻找下一个空闲的槽位。（橙色表示已被占用的槽位，黄色表示空闲槽位）
+
+![](https://static001.geekbang.org/resource/image/5c/d5/5c31a3127cbc00f0c63409bbe1fbd0d5.jpg)
+
+查找时，如果目标槽位上不是目标数据，则依次往下寻找；直至遇见目标数据或空槽位。
+
+![](https://static001.geekbang.org/resource/image/91/ff/9126b0d33476777e7371b96e676e90ff.jpg)
+
+删除时，标记为 `deleted`，而不是直接删除。
+
+#### 平方探测（Quadratic probing）
+
+插入时，如果遇到冲突，那就往后寻找下一个空闲的槽位，其步长为 $1^2$, $2^2$, $3^2$, $\ldots$。
+
+查找时，如果目标槽位上不是目标数据，则依次往下寻找，其步长为 $1^2$, $2^2$, $3^2$, $\ldots$；直至遇见目标数据或空槽位。
+
+删除时，标记为 `deleted`，而不是直接删除。
+
+#### 装载因子（load factor）
+
+$\text{load factor} = \frac{size()}{capacity()}$
+
+### 链表法
+
+所有散列值相同的 key 以链表的形式存储在同一个槽位中。
+
+![](https://static001.geekbang.org/resource/image/a4/7f/a4b77d593e4cb76acb2b0689294ec17f.jpg)
+
+插入时，不论是否有冲突，直接插入目标位置的链表。
+
+查找时，遍历目标位置的链表来查询。
+
+删除时，遍历目标位置的链表来删除。

notes/19_hashtable/readme.md

@@ -1,59 +1,59 @@
-# 散列表
-
-核心：散列表的效率并不总是 $O(1)$，仅仅是在理论上能达到 $O(1)$。实际情况中，恶意攻击者可以通过精心构造数据，使得散列表的性能急剧下降。
-
-如何设计一个工业级的散列表？
-
-## 散列函数
-
-* 不能过于复杂——避免散列过程耗时
-* 散列函数的结果要尽可能均匀——最小化散列冲突
-
-## 装载因子过大怎么办
-
-动态扩容。涉及到 rehash，效率可能很低。
-
-![](https://static001.geekbang.org/resource/image/67/43/67d12e07a7d673a9c1d14354ad029443.jpg)
-
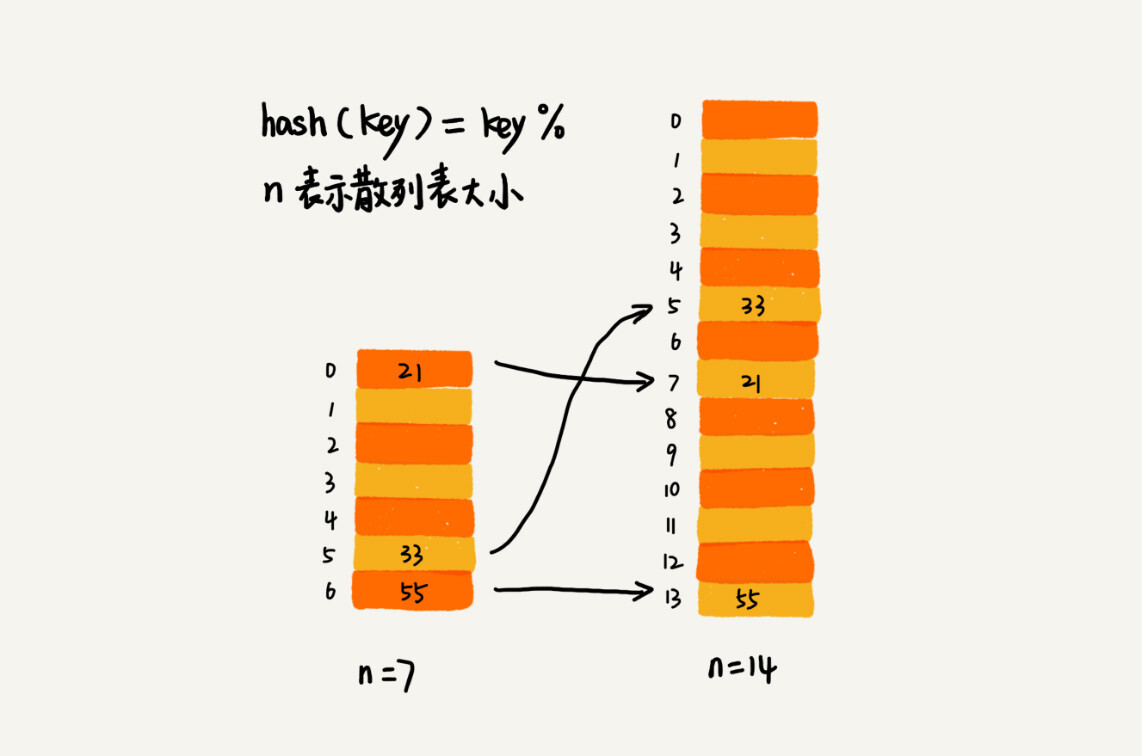-如何避免低效扩容？
-
-——将 rehash 的步骤，均摊到每一次插入中去：
-
-* 申请新的空间
-* 不立即使用
-* 每次来了新的数据，往新表插入数据
-* 同时，取出旧表的一个数据，插入新表
-
-![](https://static001.geekbang.org/resource/image/6d/cb/6d6736f986ec4b75dabc5472965fb9cb.jpg)
-
-## 解决冲突
-
-开放寻址法，优点：
-
-* 不需要额外空间
-* 有效利用 CPU 缓存
-* 方便序列化
-
-开放寻址法，缺点：
-
-* 查找、删除数据时，涉及到 `delete` 标志，相对麻烦
-* 冲突的代价更高
-* 对装载因子敏感
-
-链表法，优点：
-
-* 内存利用率较高——链表的优点
-* 对装载因子不敏感
-
-链表法，缺点：
-
-* 需要额外的空间（保存指针）
-* 对 CPU 缓存不友好
-
-——将链表改造成更高效的数据结构，例如跳表、红黑树
-
-## 举个栗子（JAVA 中的 HashMap）
-
-* 初始大小：16
-* 装载因子：超过 0.75 时动态扩容
-* 散列冲突：优化版的链表法（当槽位冲突元素超过 8 时使用红黑树，否则使用链表）
+# 散列表
+
+核心：散列表的效率并不总是 $O(1)$，仅仅是在理论上能达到 $O(1)$。实际情况中，恶意攻击者可以通过精心构造数据，使得散列表的性能急剧下降。
+
+如何设计一个工业级的散列表？
+
+## 散列函数
+
+* 不能过于复杂——避免散列过程耗时
+* 散列函数的结果要尽可能均匀——最小化散列冲突
+
+## 装载因子过大怎么办
+
+动态扩容。涉及到 rehash，效率可能很低。
+
+![](https://static001.geekbang.org/resource/image/67/43/67d12e07a7d673a9c1d14354ad029443.jpg)
+
+如何避免低效扩容？
+
+——将 rehash 的步骤，均摊到每一次插入中去：
+
+* 申请新的空间
+* 不立即使用
+* 每次来了新的数据，往新表插入数据
+* 同时，取出旧表的一个数据，插入新表
+
+![](https://static001.geekbang.org/resource/image/6d/cb/6d6736f986ec4b75dabc5472965fb9cb.jpg)
+
+## 解决冲突
+
+开放寻址法，优点：
+
+* 不需要额外空间
+* 有效利用 CPU 缓存
+* 方便序列化
+
+开放寻址法，缺点：
+
+* 查找、删除数据时，涉及到 `delete` 标志，相对麻烦
+* 冲突的代价更高
+* 对装载因子敏感
+
+链表法，优点：
+
+* 内存利用率较高——链表的优点
+* 对装载因子不敏感
+
+链表法，缺点：
+
+* 需要额外的空间（保存指针）
+* 对 CPU 缓存不友好
+
+——将链表改造成更高效的数据结构，例如跳表、红黑树
+
+## 举个栗子（JAVA 中的 HashMap）
+
+* 初始大小：16
+* 装载因子：超过 0.75 时动态扩容
+* 散列冲突：优化版的链表法（当槽位冲突元素超过 8 时使用红黑树，否则使用链表）

notes/20_hashtable/readme.md

@@ -0,0 +1,35 @@
+# 散列表
+
+散列表和链表的组合？为什么呢？
+
+* 链表：涉及查找的操作慢，不连续存储；
+* 顺序表：支持随机访问，连续存储。
+
+散列表 + 链表：结合优点、规避缺点。
+
+## 结合散列表的 LRU 缓存淘汰算法
+
+缓存的操作接口：
+
+* 向缓存添加数据
+* 从缓存删除数据
+* 在缓存中查找数据
+
+然而——不管是添加还是删除，都涉及到查找数据。因此，单纯的链表效率低下。
+
+魔改一把！
+
+![](https://static001.geekbang.org/resource/image/ea/6e/eaefd5f4028cc7d4cfbb56b24ce8ae6e.jpg)
+
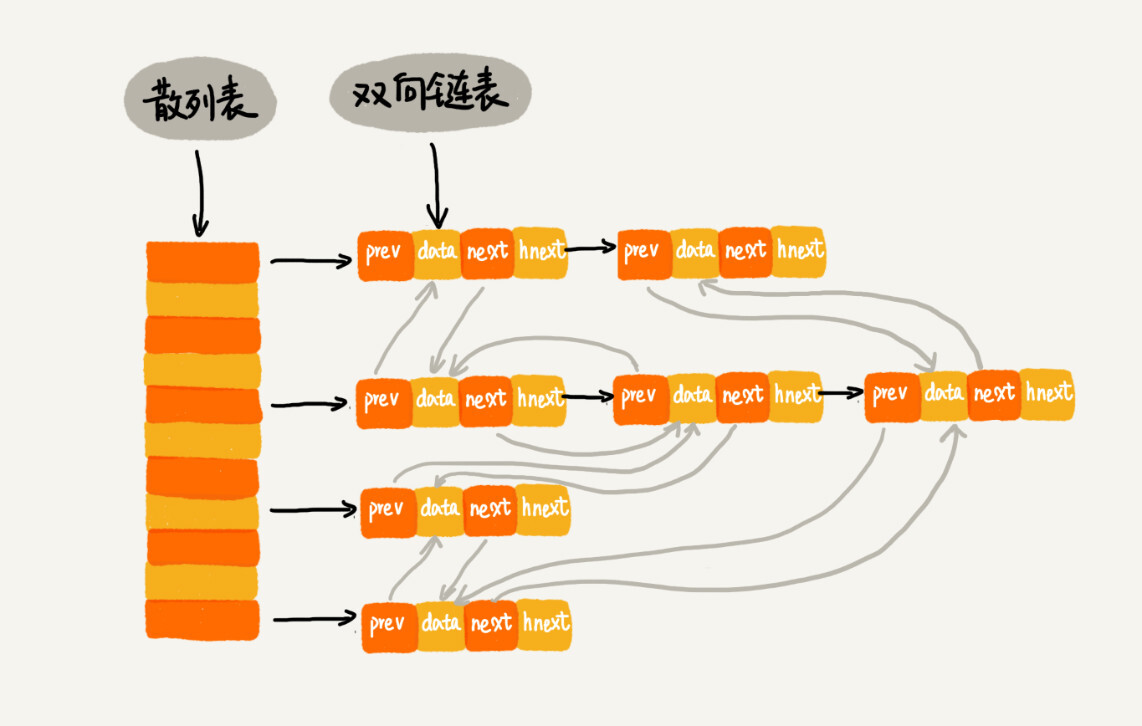+* `prev` 和 `next`：双向链表——LRU 的链表
+* `hnext`：单向链表——解决散列冲突的链表
+
+操作：
+
+* 在缓存中查找数据：利用散列表
+* 从缓存中删除数据：先利用散列表寻找数据，然后删除——改链表就好了，效率很高
+* 向缓存中添加数据：先利用散列表寻找数据，如果找到了，LRU 更新；如果没找到，直接添加在 LRU 链表尾部
+
+## Java: LinkedHashMap
+
+遍历时，按照访问顺序遍历。实现结构，与上述 LRU 的结构完全相同——只不过它不是缓存，不限制容量大小。