zCurve is a Python module with methods to efficiently map multidimensional data to a single dimension while preserving locality of the data points.
This mapping is commonly known as Z-order, Lebesgue curve, Morton space filling curve, Morton order or Morton code.
The Morton code of a multi-dimensional data point is calculated by bitwise interlacing the binary representations of its coordinate values.
zCurve provides two functions for handling the encoding and decoding of data points with arbitrary dimensionality and arbitrary coordinate size:
interlace(*data_point: int, dims: int = None, bits_per_dim: int = None) -> intdeinterlace(code_point: int, dims: int = 3) -> List[int]When handling large multi-dimensional dataset (n > 10.000), zCurve offers some simple but convenient means of parallelizing the Morton encoding and decoding:
par_interlace(data_points: List[List[int]], dims: int = None, bits_per_dim: int = None) -> List[int]par_deinterlace(code_points: List[int], dims: int = 3) -> List[List[int]]Given the Morton codes of a multi-dimensional dataset, we can perform multi-dimensional range search using only a one-dimensional data structure.
For range searching, zCurve offers two functions for calculating the necesaary LITMAX and BIGMIN values:
prev_morton(code_point: int, rmin_code: int, rmax_code: int, dims: int = 3) -> intnext_morton(code_point: int, rmin_code: int, rmax_code: int, dims: int = 3) -> intThis implementation is based on the following paper
Tropf, Herbert, and Helmut Herzog. "Multidimensional Range Search in Dynamically Balanced Trees." ANGEWANDTE INFO. 2 (1981): 71-77.
and it makes heavy use of the excellent gmpy2 module.
pip install zCurveimport zCurve as z imports the module.
code = z.interlace(2,16,8)interlaces the 3D data point (2,16,8) into Morton code point 10248.
When explicitly specify dimensionality and bits per dimension of your data point
code = z.interlace(2,16,8, dims=3, bits_per_dim=5)performance will benefit substantially.
z.deinterlace(4711)deinterlaces the Morton code point 4711 into the 3D data point (29,1,3).
Given a potentially large list of n-dimensional data_points
from random import randrange
bit_size = 16
max_val = 2**bit_size - 1
no_samples = 10**6
data_points = [(randrange(0, max_val), randrange(0, max_val), randrange(0, max_val)) for i in range(no_samples)]we can speed up things by using par_interlace and par_deinterlace
morton_codes = z.par_interlace(data_points, dims=3, bits_per_dim=16)
data_points == z.par_deinterlaces(morton_codes, dims=3)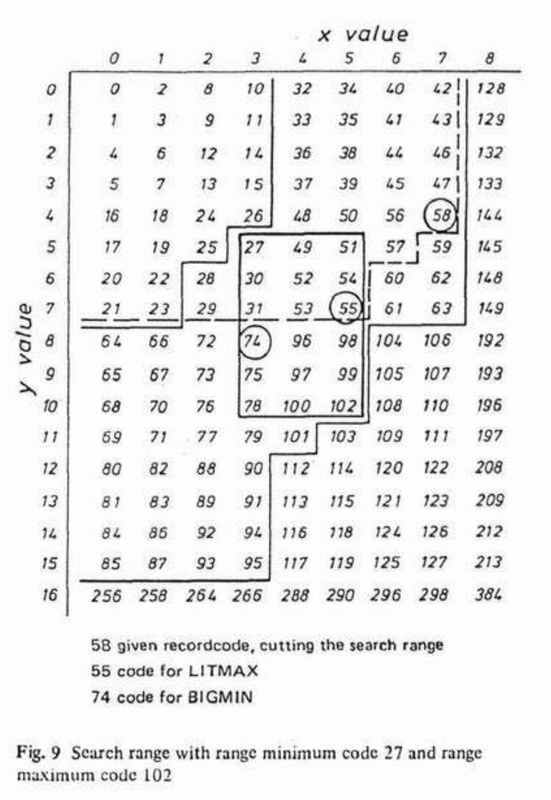
When range searching, we can prune the search space by calculating BIGMIN (aka "GetNextZ-address") and LITMAX (aka "GetPrevZ-address") values.
point = z.interlace(6, 3, dims=2) # => 30
rmin = z.interlace(5, 3, dims=2) # => 27
rmax = z.interlace(10, 5, dims=2) # => 102
BIGMIN = z.next_morton(point, rmin, rmax, dims=2) # => 31
LITMAX = z.prev_morton(point, rmin, rmax, dims=2) # => 27In addition, we can easily check if a given Morton code point is within a specified range
z.in_range(58,27,102, dims=2) # => False
z.in_range(49,27,102, dims=2) # => True@misc{rmrschub_2021_zCurve,
author = {René Schubotz},
title = {{zCurve: Multi-dimensional indexing using Morton space filling curves.}},
month = may,
year = 2021,
doi = {10.5281/zenodo.4777584},
version = {0.0.4},
publisher = {Zenodo},
url = {https://github.com/rmrschub/zCurve}
}
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
