Self-Driving Car Engineer Nanodegree Programme
This project entails the creation of an extended Kalman filter to fuse radar and lidar measurements, and to output filtered next-state estimates whilst also iteratively updating the state variables based on the current measurements, which are corrupted by noise. The goals of this project are twofold.
- Track the motion of a single object in the xy-plane in real time, based on noisy radar and lidar measurements
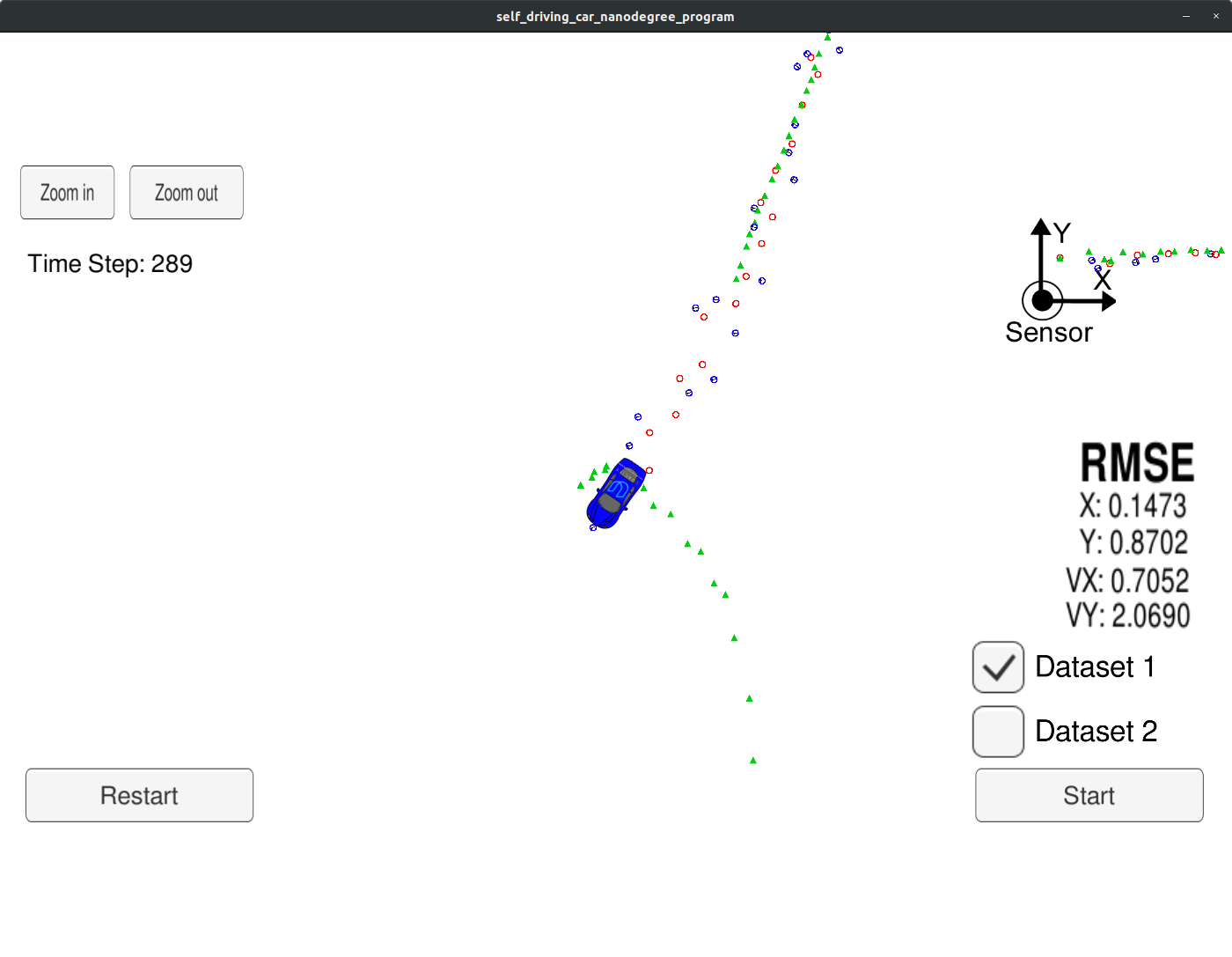
- Keep the overall root-mean-squared error (RMSE) -- for the example run using Dataset 1 -- below the prescribed thresholds of
0.11 mfor both position estimates, and0.52 m/sfor the estimated velocities, respectively
Additionally, the source files, output and results of this project must also meet the criteria laid out in the linked project rubric.
In order to succesfully compile the source code and run the executable to process the measurement data and communicate with the simulator, the following files needed to be filled in with the correct code.
- FusionEKF.cpp which initialises the EKF state variables and calls both the prediction and update methods of the
ekf_object - kalman_filter.cpp which defines the
KalmanFilterclass, of which theekf_object mentioned above is an instance, and all associated prediction and update methods, whose equations had to be filled in - tools.cpp which contains supporting methods to calculate the Jacobian matrix for the radar update equations, and also to compute the RMSE during simulation
This project was compiled and built using the default CMakeLists.txt file provided in the project starter repository.
Following a few iterations of debugging and recompiling, the executable was eventually able to successfully communicate with the simulator and generate its state predictions and updates, along with the RMSE values.
The results corresponding to Dataset 1 are shown below, and it is clear from the screenshot that the RMSE metrics from the rubric have been met.

Similarly, the following screenshot depicting simulation results corresponding to Dataset 2 is also in compliance with the RMSE criteria stipulated in the rubric.

That being said, a tricky numerical bug was the root cause for large tracking errors when the object was looping back close to the origin whilst replaying Dataset 1; this bug fix is discussed in more detail in the next section.
Whilst it was relatively straightforward to initially eliminate all syntax errors through proper declaration of all the variables and careful review of calls to member functions and their associated prototype definitions -- not to mention learning to work with the specialised VectorXd and MatrixXd data types -- it was a little bit more challenging to ascertain the root cause for a rather cryptic run-time error which cropped up even after the project was compiled successfully. An excerpt of the error message is shown below.
Assertion 'index > = 0 & & index < size()' failed. Aborted (core dumped)
It turned out this error was occurring due to some variables that had not been properly initialised within the ekf_ object -- once all vector and matrix elements were properly assigned initial values, this problem was resolved.
A more intractable problem occurred during simulation, especially with Dataset 1 -- the RMSE values were growing large too quickly, and there was a clearly distinguishable discontinuous jump during the overlapping leg of the figure eight manoeuvre right around the time the object ventured near y = 0, complete with a 180-degree flip in the heading estimate from one instant to the next, as depicted in the screenshot below.
The root cause for this bug is apparent from the documentation of the atan2() function -- specifically, whenever the trajectory is either: a) parallel or tangent to the x-axis and intersects with the y, or b) parallel or tangent to the y-axis and simultaneously intersects with the x-axis, the lack of numerical resolution in one or both arguments to this function can lead to a sudden jump between 0 and +/-π radians in case a), or a discontinuous and instantaneous jump between +/-π/2 radians in case b).
This issue is further exacerbated by the difference calculation y(1) = z(1) - φ, namely the error in the heading angle, which could see instantaneous jumps on the order of π if this issue were not addressed, and this is precisely what was happening as shown in the screen capture above.
This numerical bug was fixed by adding the following code in lines 63 to 68 of kalman_filter.cpp:
while (y(1) < -M_PI) {
y(1) += 2*M_PI;
}
while (y(1) > M_PI) {
y(1) -= 2*M_PI;
}
This code works because in a real world physical process such as a moving car or object, the changes in position as well as orientation are continuous in time (not to mention "smooth" under a suitable mathematical definition of the term) -- consequently, even upon discretisation via sampling, the expected successive changes in the sequence of position or heading errors are relatively small. Indeed, for a sufficiently small sampling interval, it is virtually impossible for an object such as a car to instantaneously flip its heading by a full π radians. Therefore, the process of iteratively adding or subtracting 2 π as appropriate, until the heading error y(1) is always restricted within the interval [-π, π] and never outside it, successfully addresses this numerical issue.
This project was a good introduction to real time sensor fusion and state estimation in the presence of additive white, Gaussian distributed measurement noise (AWGN). The concepts and techniques introduced here are invaluable in practical applications of signal processing and control algorithms in embedded systems.
A natural extension of this project would be to seek out more state of the art techniques based on the theory of nonlinear observers and robust nonlinear control of multi-input, multi-output (MIMO) systems.