| Documentation | Build Status | Community |
|---|---|---|
   |
Gridap provides a set of tools for the grid-based approximation of partial differential equations (PDEs) written in the Julia programming language. The main motivation behind the development of this library is to provide an easy-to-use framework for the development of complex PDE solvers in a dynamically typed style without sacrificing the performance of statically typed languages. The library currently supports linear and nonlinear PDE systems for scalar and vector fields, single and multi-field problems, conforming and nonconforming finite element discretizations, on structured and unstructured meshes of simplices and hexahedra.
- STABLE — Documentation for the most recently tagged version of Gridap.jl.
- DEVEL — Documentation for the in-development version of Gridap.
- ARTICLE — F. Verdugo, S. Badia. A user-guide to Gridap -- grid-based approximation of partial differential equations in Julia. arXiv. 2019. arXiv:1910.01412
Gridap is a registered package in the official Julia package registry. Thus, the installation of Gridap is straight forward using the Julia's package manager. Open the Julia REPL, type ] to enter package mode, and install as follows
pkg> add GridapA hands-on user-guide to the library is available as a set of tutorials. They are available as Jupyter notebooks and html pages.
- GridapGmsh Generate a FE mesh with GMSH and use it in Gridap.
- GridapPardiso Pluging to use the Intel Pardiso MKL direct sparse solver in Gridap.
These are some popular PDEs solved with the Gridap library. Examples taken from the Gridap Tutorials.
 |
 |
 |
 |
|---|---|---|---|
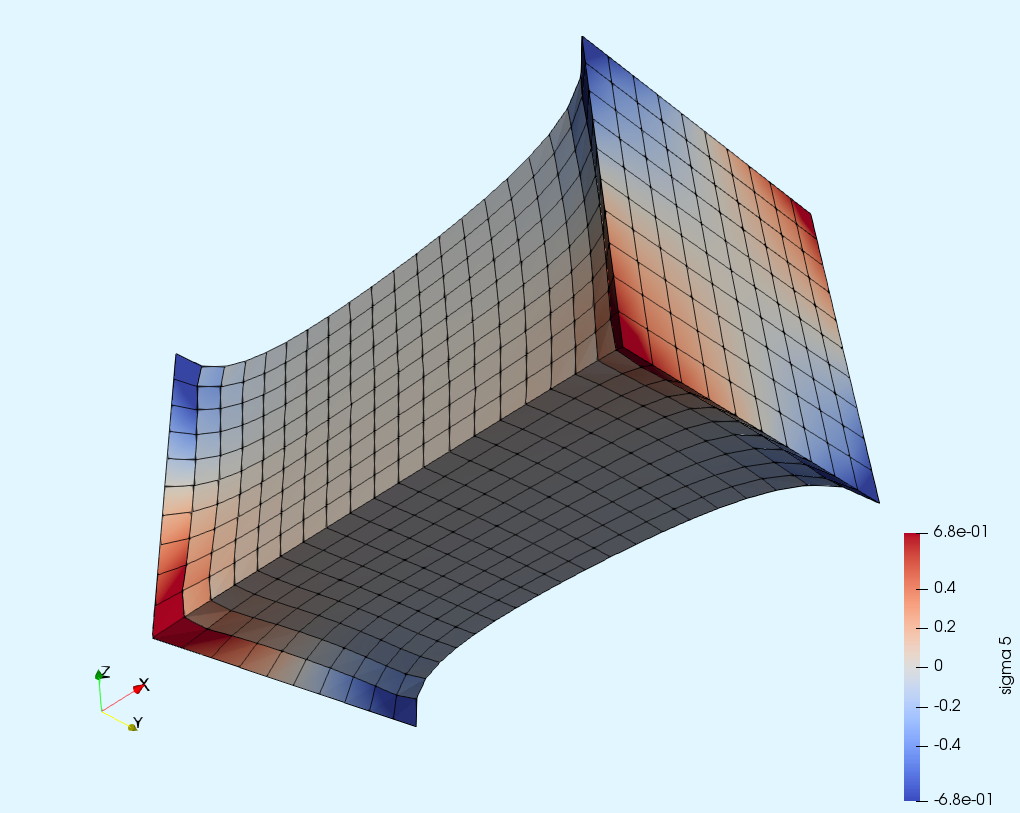
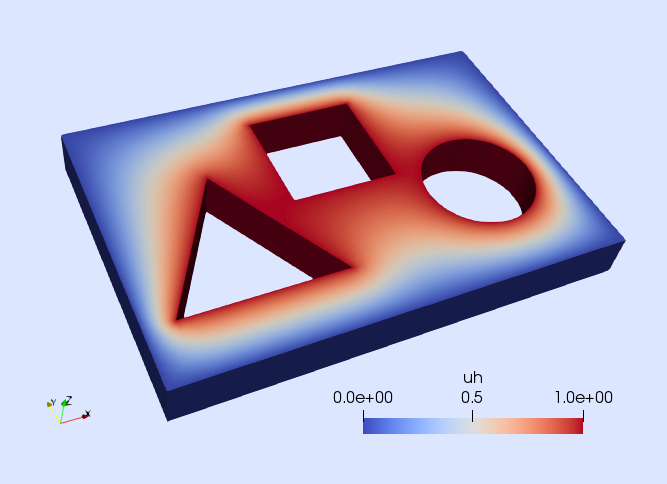
| Poisson equation | Linear elasticity | Hyper-elasticity | p-Laplacian |
 |
 |
 |
 |
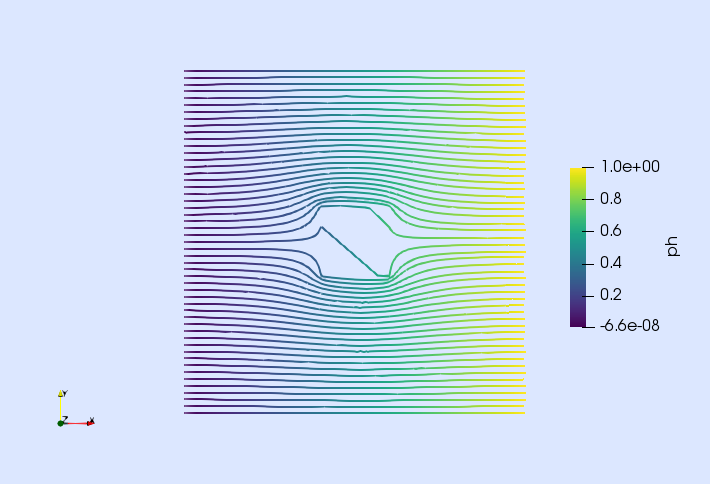
| Poisson eq. with DG | Darcy eq. with RT | Incompressible Navier-Stokes | Isotropic damage |
If you have used the Gridap library in a scientific publication, please cite the project as follows:
@article{gridap_guide_2019,
author={Francesc Verdugo and Santiago Badia},
journal = {{arXiv}},
title = {{A user-guide to Gridap -- grid-based approximation of partial differential equations in Julia}},
year = {2019},
eprint={1910.01412},
archivePrefix={arXiv},
primaryClass={cs.MS},
}