supervenn: precise and easy-to-read multiple sets visualization in Python

Installation

pip install supervenn

Requirements

Python 2.7 or 3.6+ with numpy andmatplotlib.

Note

Contrary to what the name may indicate, the diagrams produced with supervenn are not Venn diagrams in proper sense.

Basic principle

The easiest way to explain how supervenn diagrams work, is to compare some simple examples to their proper Venn counterparts:

Venn diagrams are built using the matplotlib-venn package

Basic usage

The main entry point is the eponymous supervenn function, that takes a list of python sets as its first and only required argument:

from supervenn import supervenn
sets = [{1, 2, 3, 4}, {3, 4, 5}, {1, 6, 7, 8}]
supervenn(sets, side_plots=False)

Each row is a set, the order from bottom to top is the same as in the sets list. Overlapping parts correspond to set intersections.

The numbers at the bottom show the sizes (cardinalities) of all intersections, aka chunks. The sizes of sets and their intersections (chunks) are up to proportion, but the order of elements is not preserved, e.g. the leftmost chunk of size 3 is {6, 7, 8}.

A combinatorial optimization algorithms is applied that automatically chooses an order of the chunks (the columns of the array plotted) to minimize the number of parts, the sets are broken into. In the example above there are no gaps in the rows at all, but it is not always possible even for three sets.

By default, additional side plots are also displayed:

supervenn(sets)

Here, the numbers on the right are the set sizes (cardinalities), and numbers on the top show how many sets does this intersection make part of. The grey bars represent the same numbers visually.

Most important arguments

• set_annotations: names to be displayed in each row instead of Set_0, Set_1 etc.
• figsize: the figure size in inches; calling plt.figure(figsize=(16, 10)) and supervenn afterwards will not work, because the function makes its own figure. TODO: dpi
• side_plots: True (default) or False, as shown above.
• chunks_ordering: 'minimize gaps' (default, use an quasi-greedy algorithm to to find an order of columns with fewer gaps in each row), 'size' (bigger chunks go first), 'occurence' (chunks that are in more sets go first), 'random' ( randomly shuffle the columns).
• sets_ordering: None (default - keep the order of sets as passed into function), 'minimize gaps' (use same quasi-greedy algorithm to group similar sets closer together), 'size'(bigger sets go first), 'chunk count' (sets that contain most chunks go first), 'random'.
• widths_minmax_ratio: None (default) or a number 0 < r <= 1. Useful in case the chunks (intersections) are very different in sizes. Will map the chunk sizes according to w -> a * w + b so that the minimal to maximal chunk width ratio is no smaller than widths_minmax_ratio. The exact proportionality is lost in this case. Setting widths_minmax_ratio=1 will result in all chunks being displayed as same size (no proportionality at all.)
• col_annotations_ys_count: 1 (default), 2, or 3 - also helps to reduce clutter in column annotations area.
• min_width_for_annotation: integer (default 1), another argument to reduce clutter, allows to hide annotations for chunks smaller than this value.

Other arguments can be found in the docstring to the function.

Less trivial example #1: words of different categories

letters = {'a', 'r', 'c', 'i', 'z'}
programming_languages = {'python', 'r', 'c', 'c++', 'java', 'julia'}
animals = {'python', 'buffalo', 'turkey', 'cat', 'dog', 'robin'}
geographic_places = {'java', 'buffalo', 'turkey', 'moscow'}
names = {'robin', 'julia', 'alice', 'bob', 'conrad'}
green_things = {'python', 'grass'}
sets = [letters, programming_languages, animals, geographic_places, names, green_things]
labels = ['letters', 'programming languages', 'animals', 'geographic places',
          'human names', 'green things']
supervenn(sets, labels, figsize=(10, 6), sets_ordering='minimize gaps')

And this is how the figure would look without the smart column reordering algorithm:

Less trivial example #2: banana genome compared to 5 other species

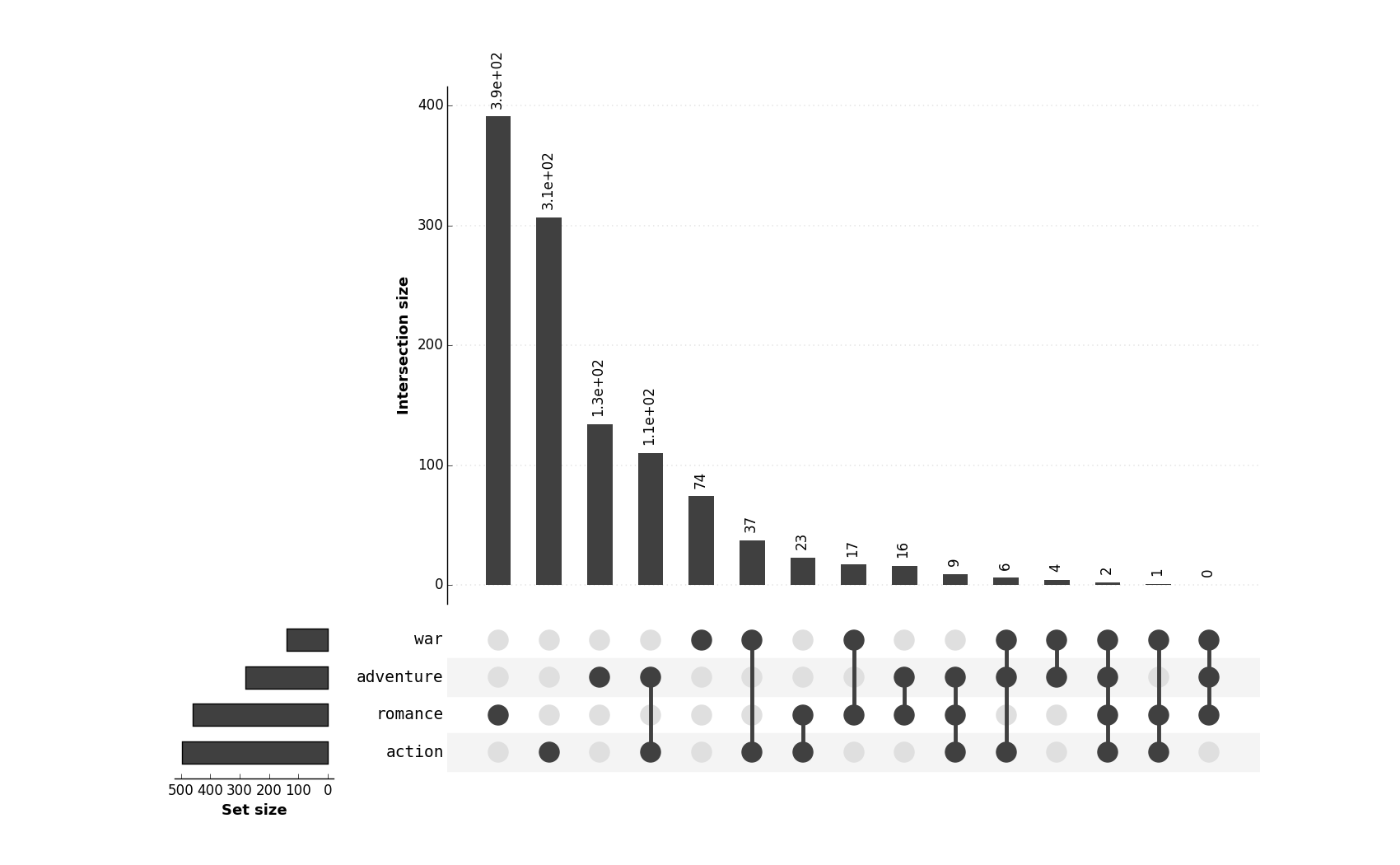
Data courtesy of Jake R Conway, Alexander Lex, Nils Gehlenborg - creators of UpSet

Image from D’Hont, A., Denoeud, F., Aury, J. et al. The banana (Musa acuminata) genome and the evolution of monocotyledonous plants

Figure from original article (note that it is by no means proportional!):

Figure made with UpSetR

Figure made with supervenn (using the widths_minmax_ratio argument)

supervenn(sets_list, species_names, figsize=(20, 10), widths_minmax_ratio=0.1,
          sets_ordering='minimize gaps', rotate_col_annotations=True, col_annotations_area_height=1.2)

For comparison, here's the same data visualized to scale (no widths_minmax_ratio, but argument min_width_for_annotation is used instead to avoid column annotations overlap):

supervenn(sets_list, species_names, figsize=(20, 10), rotate_col_annotations=True,
          col_annotations_area_height=1.2, sets_ordering='minimize gaps',
          min_width_for_annotation=180)

It must be noted that supervenn produces best results when there is some inherent structure to the sets in question. This typically means that the number of non-empty intersections is significantly lower than the maximum possible (which is 2^n_sets - 1). This is not the case in the present example, as 62 of the 63 intersections are non-empty, hence the results are not that pretty.

Less trivial example #3: order IDs in a vehicle routing problem solver tasks.

This was actually my motivation in creating this package. The team I'm currently working in provides an API that solves a variation of the Multiple Vehicles Routing Problem. The API solves tasks of the form "Given 1000 delivery orders each with lat, lon, time window and weight, and 50 vehicles each with capacity and work shift, distribute the orders between the vehicles and build an optimal route for each vehicle".

A given client can send tens of such requests per day and sometimes it is useful to look at their requests and understand how they are related to each other in terms of what orders are included in each of the request. Are they sending the same task over and over again - a sign that they are not satisfied with routes they get and they might need our help in using the API? Are they manually editing the routes (a process that results in more requests to our API, with only the orders from affected routes included)? Or are they solving for several independent order sets and are happy with each individual result?

Here's an example of a client who is not that happy:

Rows from bottom to top are requests to our API from earlier to later, represented by their sets of order IDs. With the help of some custom annotations (set_annotations argument), the situation is immediately made clear. The client solved a big task at 10:54, they were not happy about the result, and tried some manual edits until 11:11. Then in the evening they re-sent the whole task twice over, probably with some change in parameters.

Another unhappy customer:

This guy here spend almost two hours, 17:40 to 19:30 solving the same full task over and over again, with some manual edits in between. Looks like they might be doing something wrong and our help is needed.

And finally, a happy one:

Solved three unrelated tasks, was happy with all the three (no repeated requests, no manual edits; each order is distributed only once).

And here's a rather extreme example of a client whose scheme of operation involves sending requests to our API every 15-30 minutes to account for live updates on newly created orders and couriers' GPS positions: fresh data about their couriers' positions.

Algorithm used to minimize the gaps in the sets

The description of the algorithm can be found in the docstring to supervenn._algorithms module.

Comparison to similar tools

matplotlib-venn

This tool plots area-weighted Venn diagrams with circles for two or three sets. But the problem with circles is that they are pretty useless even in the case of three sets. For example, if one set is symmetrical difference of the other two:

from matplotlib_venn import venn3
set_1 = {1, 2, 3, 4}
set_2 = {3, 4, 5}
set_3 = set_1 ^ set_2
venn3([set_1, set_2, set_3], set_colors=['steelblue', 'orange', 'green'], alpha=0.8)

See all that zeros? This image makes little sense. The supervenn's approach to this problem is to allow the sets to be broken into separate parts, while trying to minimize the number of such breaks and guaranteeing exact proportionality of all parts:

UpSetR and pyUpSet

This approach, while very powerful, is less visual, as it displays, so to say only _statistics about_ the sets, not the sets in flesh.

pyvenn

This package produces diagrams for up to 6 sets, but they are not in any way proportional. It just has pre-set images for every given sets count, your actual sets only affect the labels that are placed on top of the fixed image, not unlike the banana diagram above.

RainBio (article)

This approach is quite similar to supervenn. I'll let the reader decide which one does the job better:

RainBio:

supervenn:

Thanks to Dr. Bilal Alsallakh for referring me to this work

Linear Diagram Generator

This tool has a similar concept, but only available as a Javascript web app with minimal functionality, and you have to compute all the intersection sizes yourself. Apparently there is also an columns rearrangement algorithm in place, but the target function (number of gaps within sets) is higher than in the diagram made with supervenn.

Thanks to u/aboutscientific for the link.

Plans for future releases

• Tuning of the randomized algorithm for more optimal results (experiments are underway).
• Implement some way to inspect individual intersections (probably label them with alphabetic codes like columns in Excel tables, and supervenn function returns a dict with these codes as keys and intersection sets as values).
• Tests for the _plots module.
• Web-based app for non-pythonistas.

Author

This package is created and maintained by Fedor Indukaev. This is my first attempt at making a full Python package, so code and structure of the package might be not up to best practices sometimes. Any bug reports, questions, comments, recommendations, feature requests, pull requests, code reviews etc are most welcome. My username on Gmail and Telegram is the same as on Github.