Directional Diffusion Models

NeurIPS 2023

Run Yang¹, Yuling Yang¹, Fan Zhou¹, Qiang Sun^2
1Shanghai University of Finance and Economics, ²University of Toronto

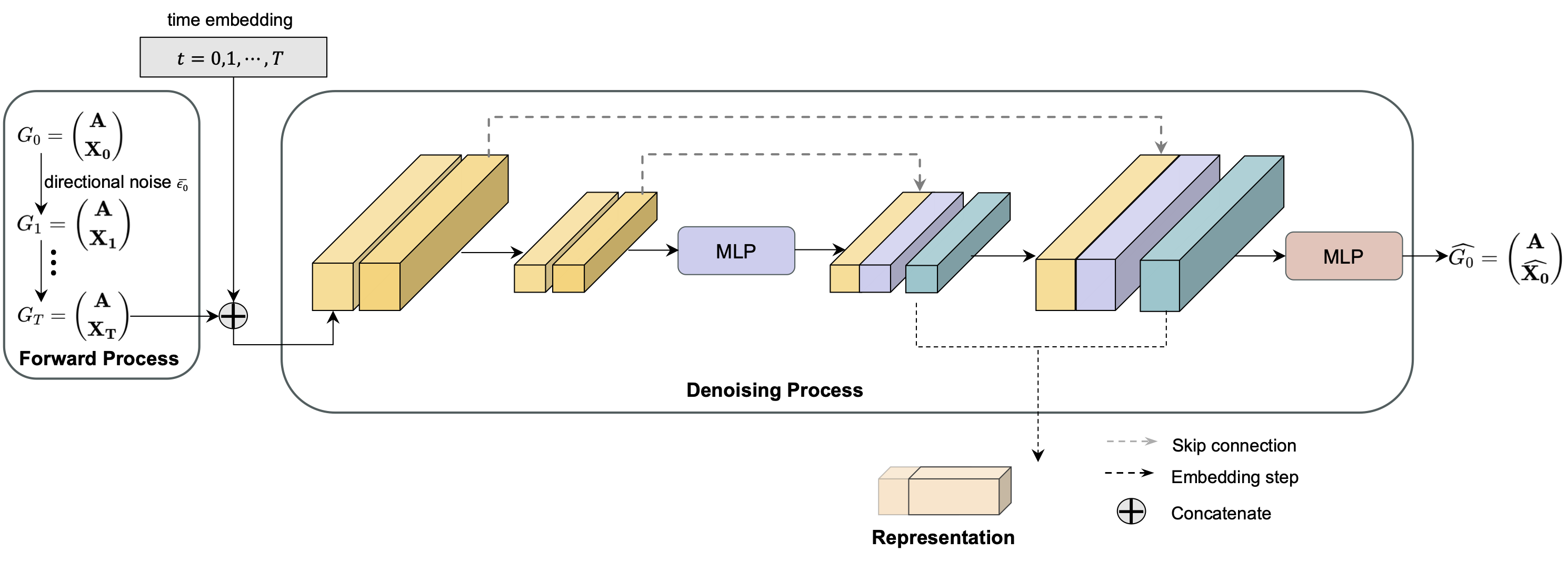
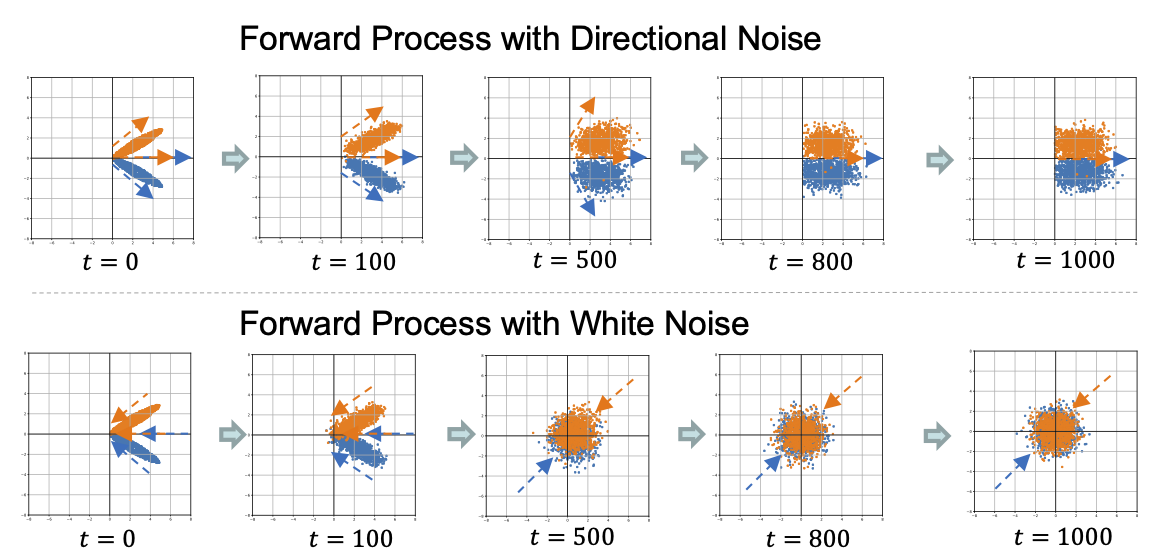
We introduce a novel class of models termed directional diffusion models (DDM), which adopt data-dependent, anisotropic, and directional noises in the forward diffusion process. This code is an implementation of DDM on 12 public graph datasets.

Graph classification datasets

• IMDB-B
• IMDB-M
• COLLAB
• REDDIT-B
• PROTEINS
• MUTAG

Node classification datasets

• CORA
• Citeseer
• PubMed
• Ogbn-arxiv
• Amazon-Computer
• Amazon-Photo

Framework

Usage

conda create -n ddm python=3.8
conda activate ddm
cd ddm-nni
pip install -r requirements.txt

cd to EXP path(MUTAG for example)

cd GraphExp
python main_graph.py --yaml_dir ./yamls/MUTAG.yaml

In view of the sensitivity of diffusion method to hyperparameters, it is recommended to use hyperparameter search methods like NNI to achieve better results Trust me ! In this way, you can achieve better results than what is presented in the paper

Performance

Directional noise v.s. white noise

Graph classification(F1-score)

	IMDB-B	IMDB-M	COLLAB	REDDIT-B	PROTEINS	MUTAG
GIN[1]	75.1±5.1	52.3±2.8	80.2±1.9	92.4±2.5	76.2±2.8	89.4±5.6
DiffPool[2]	72.6±3.9	-	78.9±2.3	92.1±2.6	75.1±2.3	85.0±10.3
Infograph[3]	73.03±0.87	49.69±0.53	70.65±1.13	82.50±1.42	74.44±0.31	89.01±1.13
GraphCL[4]	71.14±0.44	48.58±0.67	71.36±1.15	89.53±0.84	74.39±0.45	86.80±1.34
JOAO[5]	70.21±3.08	49.20±0.77	69.50±0.36	85.29±1.35	74.55±0.41	87.35±1.02
GCC[6]	72	49.4	78.9	89.8	-	-
MVGRL[7]	74.20±0.70	51.20±0.50	-	84.50±0.60	-	89.70±1.10
GraphMAE[8]	75.52±0.66	51.63±0.52	80.32±0.46	88.01±0.19	75.30±0.39	88.19±1.26
DDM	76.40±0.22	52.53±0.31	81.72±0.31	89.15±1.3	75.74±0.50	91.51±1.45

Node classification(F1-score)

Dataset	Cora	Citeseer	PubMed	Ogbn-arxiv	Computer	Photo
GAT	83.0 ± 0.7	72.5 ± 0.7	79.0 ± 0.3	72.10 ± 0.13	86.93 ± 0.29	92.56 ± 0.35
DGI[9]	82.3 ± 0.6	71.8 ± 0.7	76.8 ± 0.6	70.34 ± 0.16	83.95 ± 0.47	91.61 ± 0.22
MVGRL[7]	83.5 ± 0.4	73.3 ± 0.5	80.1 ± 0.7	-	87.52 ± 0.11	91.74 ± 0.07
BGRL[10]	82.7 ± 0.6	71.1 ± 0.8	79.6 ± 0.5	71.64 ± 0.12	89.68 ± 0.31	92.87 ± 0.27
InfoGCL[11]	83.5 ± 0.3	73.5 ± 0.4	79.1 ± 0.2	-	-	-
CCA-SSG[12]	84.0 ± 0.4	73.1 ± 0.3	81.0 ± 0.4	71.24 ± 0.20	88.74 ± 0.28	93.14 ± 0.14
GPT-GNN[13]	80.1 ± 1.0	68.4 ± 1.6	76.3 ± 0.8	-	-	-
GraphMAE[8]	84.2 ± 0.4	73.4 ± 0.4	81.1 ± 0.4	71.75 ± 0.17	88.63 ± 0.17	93.63 ± 0.22
DDM	83.4±0.2	74.3±0.3	81.7±0.8	71.29±0.18	90.56±0.21	95.09±0.18

References

[1]:Xu, K., Hu, W., Leskovec, J., and Jegelka, S. (2018). How powerful are graph neural networks? arXiv preprint arXiv:1810.00826.
[2]:Ying, Z., You, J., Morris, C., Ren, X., Hamilton, W., and Leskovec, J. (2018). Hierarchical graph representation learning with differentiable pooling. Advances in neural information processing systems, 31.
[3]:Sun, F.-Y., Hoffmann, J., Verma, V., and Tang, J. (2019). Infograph: Unsupervised and semi- supervised graph-level representation learning via mutual information maximization. arXiv preprint arXiv:1908.01000.
[4]:You, Y., Chen, T., Sui, Y., Chen, T., Wang, Z., and Shen, Y. (2020). Graph contrastive learning with augmentations. Advances in neural information processing systems, 33:5812–5823.
[5]:You, Y., Chen, T., Shen, Y., and Wang, Z. (2021). Graph contrastive learning automated. In International Conference on Machine Learning, pages 12121–12132. PMLR.
[6]:Qiu, J., Chen, Q., Dong, Y., Zhang, J., Yang, H., Ding, M., Wang, K., and Tang, J. (2020). Gcc: Graph contrastive coding for graph neural network pre-training. In Proceedings of the 26th ACM SIGKDD international conference on knowledge discovery & data mining, pages 1150–1160.
[7]:Hassani, K. and Khasahmadi, A. H. (2020). Contrastive multi-view representation learning on graphs. In International conference on machine learning, pages 4116–4126. PMLR.
[8]:Hou, Z., Liu, X., Dong, Y., Wang, C., Tang, J., et al. (2022). Graphmae: Self-supervised masked graph autoencoders. arXiv preprint arXiv:2205.10803.
[9]:Velickovic, P., Fedus, W., Hamilton, W. L., Liò, P., Bengio, Y., and Hjelm, R. D. (2019). Deep graph infomax. ICLR (Poster), 2(3):4.
[10]:Thakoor, S., Tallec, C., Azar, M. G., Azabou, M., Dyer, E. L., Munos, R., Veliˇckovi ́c, P., and Valko, M. (2021). Large-scale representation learning on graphs via bootstrapping. arXiv preprint arXiv:2102.06514.
[11]:Xu, D., Cheng, W., Luo, D., Chen, H., and Zhang, X. (2021). Infogcl: Information-aware graph contrastive learning. Advances in Neural Information Processing Systems, 34:30414–30425.
[12]:Zhang, H., Wu, Q., Yan, J., Wipf, D., and Yu, P. S. (2021). From canonical correlation analysis to self-supervised graph neural networks. Advances in Neural Information Processing Systems, 34:76–89.
[13]:Hu, Z., Dong, Y., Wang, K., Chang, K.-W., and Sun, Y. (2020b). Gpt-gnn: Generative pre-training of graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 1857–1867.