[notes][12_sorts] merge sort, done.

notes/12_sorts/readme.md

@@ -0,0 +1,80 @@
+# 排序（线性对数时间复杂度排序算法）
+
+开篇问题：如何在 $O(n)$ 时间复杂度内寻找一个无序数组中第 K 大的元素？
+
+## 归并排序
+
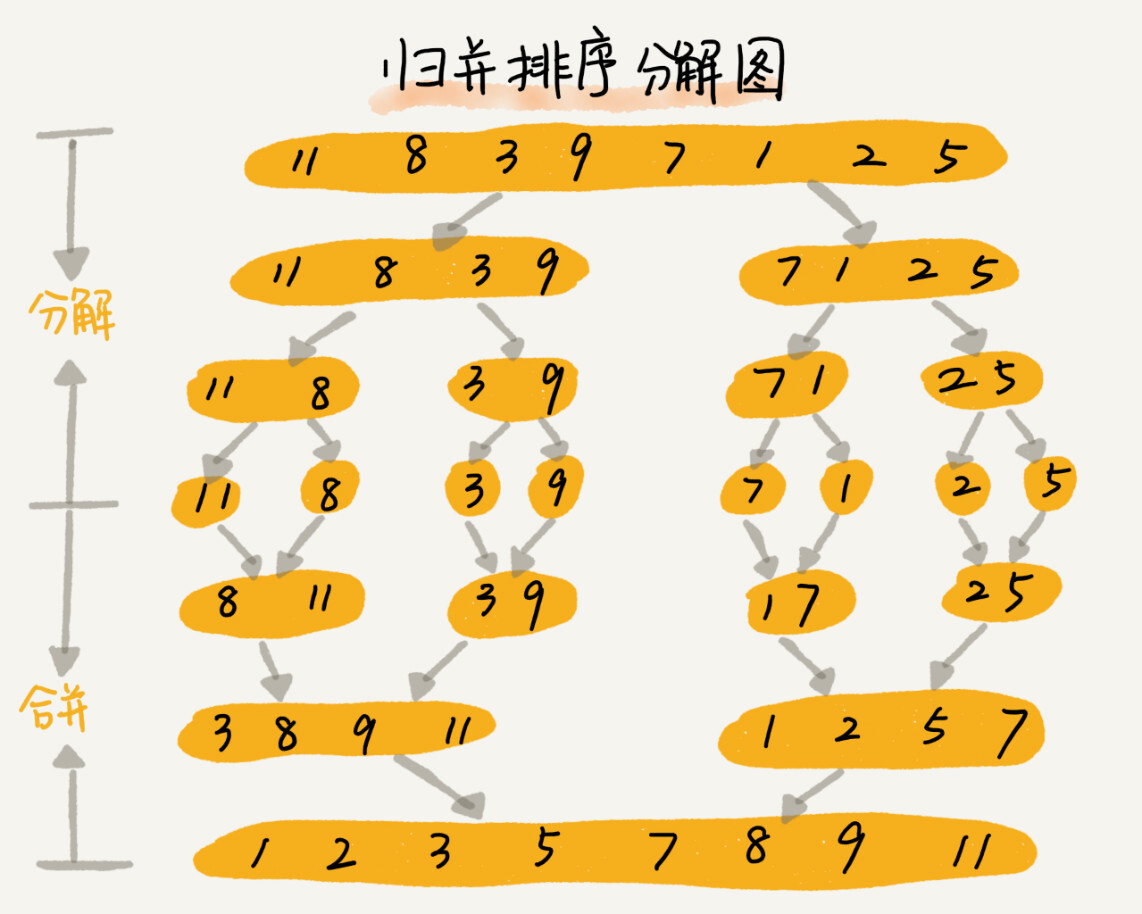
+* 归并排序使用了「分治」思想（Divide and Conquer）
+    * 分：把数组分成前后两部分，分别排序
+    * 合：将有序的两部分合并
+
+![归并排序分解图](https://static001.geekbang.org/resource/image/db/2b/db7f892d3355ef74da9cd64aa926dc2b.jpg)
+
+* 分治与递归
+    * 分治：解决问题的处理办法
+    * 递归：实现算法的手段
+    * ——分治算法经常用递归来实现
+* 递归实现：
+    * 终止条件：区间 `[first, last)` 内不足 2 个元素
+    * 递归公式：`merge_sort(first, last) = merge(merge_sort(first, mid), merge_sort(mid, last))`，其中 `mid = first + (last - first) / 2`
+
+C++ 实现：
+
+```cpp
+template <typename FrwdIt,
+          typename T = typename std::iterator_traits<FrwdIt>::value_type,
+          typename BinaryPred = std::less<T>>
+void merge_sort(FrwdIt first, FrwdIt last, BinaryPred comp = BinaryPred()) {
+    const auto len = std::distance(first, last);
+    if (len <= 1) { return; }
+    auto cut = first + len / 2;
+    merge_sort(first, cut, comp);
+    merge_sort(cut, last, comp);
+    std::vector<T> tmp;
+    tmp.reserve(len);
+    detail::merge(first, cut, cut, last, std::back_inserter(tmp), comp);
+    std::copy(tmp.begin(), tmp.end(), first);
+}
+```
+
+这里涉及到一个 `merge` 的过程，它的实现大致是：
+
+```cpp
+namespace detail {
+template <typename InputIt1, typename InputIt2, typename OutputIt,
+          typename BinaryPred = std::less<typename std::iterator_traits<InputIt1>::value_type>>
+OutputIt merge(InputIt1 first1, InputIt1 last1,
+               InputIt2 first2, InputIt2 last2,
+               OutputIt d_first,
+               BinaryPred comp = BinaryPred()) {
+    for (; first1 != last1; ++d_first) {
+        if (first2 == last2) {
+            return std::copy(first1, last1, d_first);
+        }
+        if (comp(*first2, *first1)) {
+            *d_first = *first2;
+            ++first2;
+        } else {
+            *d_first = *first1;
+            ++first1;
+        }
+    }
+    return std::copy(first2, last2, d_first);
+}
+}  // namespace detail
+```
+
+![`merge` 的过程](https://static001.geekbang.org/resource/image/95/2f/95897ade4f7ad5d10af057b1d144a22f.jpg)
+
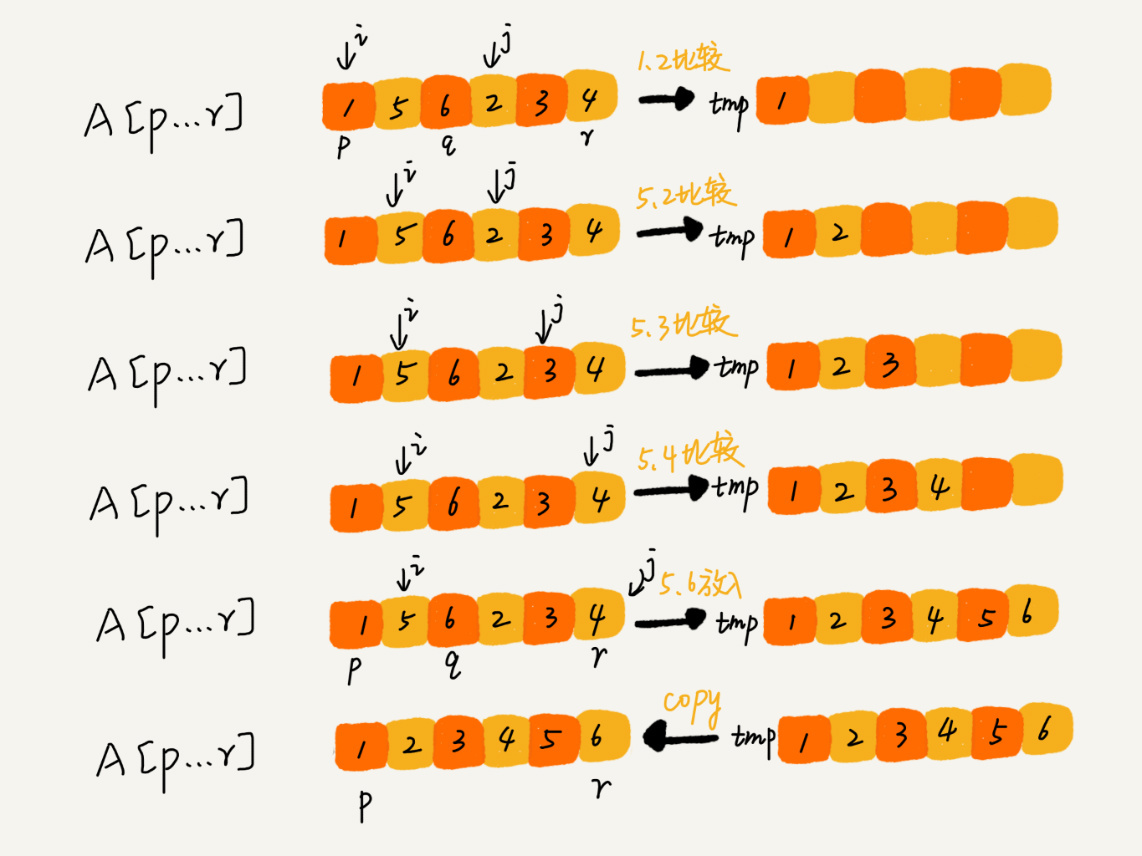+### 算法分析
+
+* 稳定性
+    * 由于 `comp` 是严格偏序，所以 `!comp(*first2, *first1)` 时，取用 `first1` 的元素放入 `d_first` 保证了算法稳定性
+* 时间复杂度
+    * 定义 $T(n)$ 表示问题规模为 $n$ 时算法的耗时，
+    * 有递推公式：$T(n) = 2T(1/2) + n$
+    * 展开得 $T(n) = 2^{k}T(1) + k * n$
+    * 考虑 $k$ 是递归深度，它的值是 $\log_2 n$，因此 $T(n) = n + n\log_2 n$
+    * 因此，归并排序的时间复杂度为 $\Theta(n\log n)$
+* 空间复杂度
+    * 一般来说，空间复杂度是 $\Theta(n)$