ATcalculation

AT system calculation by python 牵引供电系统计算软件

平行多导线系统参数计算函数 '

'

编写人： 陈剑云

1 多导线原始参数

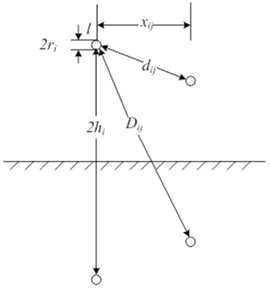
牵引网导线架设横截面示意图

导线编号：

导线号	导线代码	导线名称
01	CW1	接触导线1
02	MW1	承力索1
03	PF1	正馈线1
04	RA1	钢轨1
05	RA2	钢轨2
06	PW1	保护线1
07	E1	综合地线1
08	CW2	接触导线2
09	MW2	承力索2
10	PF2	正馈线2
11	RA3	钢轨3
12	RA4	钢轨4
13	PW2	保护线2
14	E2	综合地线2

导线架设截面坐标

conductors_coordinater=0.001*np.array([[0,6300],[0,7500],[-4400,8500],[-755,1000],[755,1000],[-3600,8000],[-4400,500], [5000,6300],[5000,7500],[4400+5000,8500],[4245,1000],[5755,1000],[3600+5000,8000], [4400+5000,500]],np.float64) # 多导体坐标数组 (x,y),单位 m

导线计算半径： conductors_calc_radius=0.001np.array([5.9,7.00,9.5,109.1,109.1,7.60,5.35,5.9,7.00,9.5,109.1,109.1,7.60,5.35]) #多导体计算半径，单位 m， 计算电位系数用 导线等效半径： conductors_equivalent_radius=0.001np.array([4.2,5.31,9.03,12.79,12.79,7.22,4.055,4.2,5.31,9.03,12.79,12.79,7.22,4.055]) #多导体等效半径,单位m, 计算自电感用 导线直流电阻： conductors_resistance=np.array([0.146,0.158,0.163,0.135,0.135,0.255,0.28,0.146,0.158,0.163,0.135,0.135,0.255,0.28]) #多导体直流电阻，单位 欧/km

{原始参数在软件开发前期用数组形式给出，在后阶段以数据文件的形式存储，通过读取数据生成变量。}

2 电位系数矩阵计算

函数名： calc_potential_coefficient(c_xy,r)

• parameters:
  1. c_xy: 2×n维数组，多导线的坐标（x,y）,单位(m);
  2. r: 1×n维数组，导线的半径,单位(m)
• Return: 1. P: n×n维数组，电位系数，单位$(K/km)^{-1}$
• 功能： 计算多导体的电位系数矩阵P。

计算公式：

$$ P_{ii}=\frac{1}{2\pi\epsilon}ln\frac{2h_{i}}{r_i}=18×10^６ln\frac{2h_{i}}{r_i}$$

$$ P_{ij}=\frac{1}{2\pi\epsilon}ln\frac{D_{ij}}{d_{ij}}=18×10^６ln\frac{D_{ij}}{d_{ij}} ~~~~ (i≠j) $$

其中$\epsilon_0$为空气介电系数，单位(F/km) $$\epsilon_0=\frac{1}{36\pi 10^6}$$

3 导线合并，求合并后的电位系数

** 函数名: merge_potential_coefficient(P,m,k)**

• parameters:
  1. P: n×n 维数组，电位系数 ;
  2. m: 第 m 号导线（导线序号从0开始）； 3. k: 第 k 号导线，m＜k≤n,

• Return: 1. P: n-1×n-1 维数组，归并后的电位系数

• 功能： 导线k并入导线m,计算修正后的电位系数P

导线k并入m公式推导：

\begin{equation} \begin{bmatrix} u_1\ \vdots\ u_m\ \vdots\ u_k\ \vdots\ u_n \end{bmatrix}= \begin{bmatrix} P_{11}&\dots& P_{1m}&\dots&P_{1k}&\dots&P_{1n}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{m1}&\dots& P_{mm}&\dots&P_{mk}&\dots&P_{mn}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{k1}&\dots& P_{km}&\dots&P_{kk}&\dots&P_{kn}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{n1}&\dots& P_{nm}&\dots&P_{nk}&\dots&P_{nn}\ \end{bmatrix} \begin{bmatrix} q_1\ \vdots\ q_m\ \vdots\ q_k\ \vdots\ q_n \end{bmatrix} \end{equation}

令 $q_{m}=q_{m}+q_{k}$ 有：

\begin{equation} \begin{bmatrix} u_1\ \vdots\ u_m\ \vdots\ u_k\ \vdots\ u_n \end{bmatrix} = \begin{bmatrix} P_{11}&\dots& P_{1m}&\dots&(P_{1k}-P_{1m})&\dots&P_{1n}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{m1}&\dots& P_{mm}&\dots&(P_{mk}-P_{mm})&\dots&P_{mn}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{k1}&\dots& P_{km}&\dots&(P_{kk}-P_{km})&\dots&P_{kn}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{n1}&\dots& P_{nm}&\dots&(P_{nk}-P_{nm})&\dots&P_{nn}\ \end{bmatrix} \begin{bmatrix} q_1\ \vdots\ q_m+q_k\ \vdots\ q_k\ \vdots\ q_n \end{bmatrix} \end{equation}

P矩阵第k列参数发生变化，修正公式为：$$P_{ik}=P_{ik}-P_{im} ( i=1,...,n), q_m=q_m+q_k$$.

方程中，$u_{k}-u_{m}=0$,得方程

\begin{equation*} \begin{bmatrix} u_1\ \vdots\ u_m\ \vdots\ 0\ \vdots\ u_n \end{bmatrix} = \begin{bmatrix} P_{11}&\dots& P_{1m}&\dots&P_{1k}&\dots&P_{1n}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{m1}&\dots& P_{mm}&\dots&P_{mk}&\dots&P_{mn}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{k1}- P_{m1}&\dots& P_{km}-P_{mm}&\dots&P_{kk}-P_{mk}&\dots&P_{kn}-P_{mn}\ \vdots& &\vdots& &\vdots& &\vdots\ P_{n1}&\dots& P_{nm}&\dots&P_{nk}&\dots&P_{nn}\ \end{bmatrix} \begin{bmatrix} q_1\ \vdots\ q_m\ \vdots\ q_k\ \vdots\ q_n \end{bmatrix} \end{equation*}

第k行等式有: $$ 0= (P_{k1}- P_{m1})q_1+\dots+（P_{km}-P_{mm})q_m+\dots+(P_{kk}-P_{mk})q_k+\dots+(P_{kn}-P_{mn})q_n$$

可以求得： $$q_k=-\frac{(P_{k1}- P_{m1})}{(P_{kk}-P_{mk})}q_1-\dots-\frac{(P_{km}- P_{mm})}{(P_{kk}-P_{mk})}q_m\dots-\frac{(P_{kn}- P_{mn})}{(P_{kk}-P_{mk})}q_n$$

令$K_j=\frac{P_{kj}- P_{mj}}{P_{kk}-P_{mk}}$ (j≠k)，有 $$q_k=-K_1q_1-\dots-K_m q_m-\dots-K_n q_n$$

导线电压$u_i$写成方程有： $$u_i=P_{i1}q_1+\dots+P_{im}q_m+\dots+P_{ik}q_k+\dots+P_{in}q_n$$

把$q_k$代入方程中，得到 $$u_i=（P_{i1}-P_{ik}K_1)q_1+\dots+(P_{im}-P_{ik}K_m)q_m+\dots+(P_{in}-P_{ik}K_n)q_n$$

取(i,j=0,1,...,n; i≠k;j≠k),可以得到合并矩阵元素$P_{ij}$. $$P_{ij}=P_{ij}-P_{ik}K_j=P_{ij}-P_{ik}\frac{P_{kj}- P_{mj}}{P_{kk}-P_{mk}}$$

总之，导线k合并到导线m，P参数的修正步骤归纳如下：

（1）$P_{ik}=P_{ik}-P_{im}$ ( i=1,...,n)

（2）$P_{ij}=P_{ij}-P_{ik}K_j=P_{ij}-P_{ik}\frac{P_{kj}- P_{mj}}{P_{kk}-P_{mk}}$ （i,j=1,...,n; i≠k;j≠k）

（3）除P中的第k行第k列，P降n-1阶，为合并后n-1根导线的电位系数矩阵。

例

AT牵引网络由14根导线逐步合并成6根导线：

（1） 1. 接触线（CW1）+ 2.承力索（MW1）

（2） 3.正馈线（PF1）

（3） 4.钢轨1（RA1）+5.钢轨2（RA2）+6.保护线（PW1）+7.综合地线（E1）

（4） 8. 接触线（CW2）+ 9.承力索（MW2）

（5） 10.正馈线（PF2）

（6） 11.钢轨3（RA3）+12.钢轨4（RA4）+13.保护线（PW2）+14.综合地线（E2）

4 电容系数矩阵计算

函数名： calc_B(P)

5 理想导体时电感L矩阵计算

函数名：calc_L(c_xy,r)

• Parameters:

  1. c_xy: 2×n维数组，多导线的坐标（x,y）,单位（m）;
  2. r: 1×n维数组，导线的半径,单位(m)

• Return:

  1. L: n×n维数组，多导体和大地为理想导体时的自感$L_{ii}$和互感$L_{ij}$ (H/km)

功能： 计算理想导体时的自感$L_{ii}$和互感$L_{ij}$

计算公式：

导线回路电感 $$L_{ii}=\frac{\mu_0}{2\pi}ln\frac{2h_i}{r_i}=2×10^{-4}ln\frac{2h_i}{r_i}$$ 导线回路互感 $$L_{ij}=\frac{\mu_0}{2\pi}ln\frac{D_{ij}}{d_{ij}}=2×10^{-4}ln\frac{D_{ij}}{d_{ij}}$$

其中　$$\mu_0=4\pi10^{-4} (H/km)$$

6 计算导线内电阻和内电感

函数名： calc_Zc(f,Rd,r,rho,mu_r)

• Parameters:

  1. f: 频率（Hz）
  2. Rd: 1xn 维，导线直流电阻，（Ω/km） 3 r: 1xn维，导线半径（m）
  3. rho: １xn维　导线电阻率，（Ω/m）
  4. mu_r: 1xn维　导线导磁率，（H/km)

• Return:

  1. Rc: １×n维 导线交流电阻（Ω/km）
  2. Xc: 1xn维　导线交流内电感（H/km）

功能：计算导线的交流电阻Rc和内电感Lc

计算方法１： 实心圆柱体单位长度交流内阻抗为
$$ Z_c=\frac{jmρJ_0(nr)}{2\pi J_1(nr)}=\frac{jmρ}{2\pi r}\frac{ber(mr)+jbei(mr)}{ber'(mr)+jbei'(mr)}$$ 式中$n=jm\sqrt j ,m=\sqrt\frac{\omega\mu}{\rho}$

计算方法２： 　公式

$$ Z_c=R_c+j\omega L_c$$

$$ R_c=\alpha_R R_d=\alpha_R\frac{\rho}{\pi r^2}$$

$$ L_c=\alpha_LL_d=\alpha_L\frac{\mu_r\mu_0}{8\pi}=\frac{\mu_r}{2}.10^{-4}\alpha_L$$ 其中 $$\alpha_R=\frac{mr}{2}[\frac{beimr.bei'mr-bermr.ber'mr}{(ber'mr)^2+(bei'mr)^2}]$$

$$\alpha_L=\frac{4}{mr}[\frac{bermr.bei'mr+bermr.ber'mr}{(ber'mr)^2+(bei'mr)^2}]$$

导线内阻一般用上述基于贝塞尔函数的公式计算。对于一般导线，其导磁率取$\mu_0$，如果导线是钢轨，由于是铁磁材质，其导磁率$\mu$为$\mu_r\mu_0$,其数值需要钢轨磁滞曲线给出。若考虑钢轨是非规则截面导体，其精确的阻抗需要通过用有限元软件计算给出。

7 计算大地与导线回路电阻和电感

函数名：calc_Zgm(f,c_xy，rou)

• Parameters:
  1. f: 频率（Hz）
  2. c_xy: 2×n维数组，多导线的坐标（x,y）,单位（m）;
  3. rou: 大地电阻率（Ω/m）
• Return:
  1. Rgm: n×n维数组,大地与导线回路电阻（Ω/km）
  2. Xgm: n×n维数组,大地与导线回路感抗（Ω/km）

功能：计算导线与大地的互阻抗,需要调用函数calc_Rg()，calc_Xg()

8 频变阻抗矩阵计算

** calc-Zf(f,c_xy,r,Rd,rou) **

• Parameters:

  1. f: 频率（Hz）
  2. c_xy: 2×n维数组，多导线的坐标（x,y）,单位（m）;
  3. r: 1×n维数组，导线计算半径（m）
  4. Rd 1×n维数组，导线直流电阻
  5. rou 大地电阻率（Ω/m）

• Return:

  1. Zf: 导线频变阻抗矩阵

9 简化阻抗矩阵计算

** calc_z(f,c_xy,re,Rd,rou)**

• Parameters:
  1. f: 频率（Hz）
  2. c_xy: 2×n维数组，多导线的坐标（x,y）,单位（m）;
  3. re: 1×n维数组导线，等效半径（m）
  4. Re 1×n维数组，导线电阻
  5. rou 大地电阻率（Ω/m）
• Return:
  1. R: 导线交流电阻（Ω/m）
  2. X: 导线交流内电感（亨/km）
  3. z: 导线阻抗矩阵

10 阻抗矩阵合并

** 函数名：merge_z(z,m,k)**

• parameters:
  1. z: n×n 维数组，阻抗矩阵 ;
  2. m: 第 m 号导线（导线序号从0开始）； 3. k: 第 k 号导线，m＜k≤n,
• Return: 1. z: n-1×n-1 维数组，归并后的电位系数

功能： 导线k并入导线m, k＜m≤n, n为z的阶，输出合并阻抗矩阵z,z降一阶

AT牵引网络由14根导线逐步合并成6根导线：

（1） 1. 接触线（CW1）+ 2.承力索（MW1）

（2） 3.正馈线（PF1）

（3） 4.钢轨1（RA1）+5.钢轨2（RA2）+6.保护线（PW1）+7.综合地线（E1）

（4） 8. 接触线（CW2）+ 9.承力索（MW2）

（5） 10.正馈线（PF2）

（6） 11.钢轨3（RA3）+12.钢轨4（RA4）+13.保护线（PW2）+14.综合地线（E2）