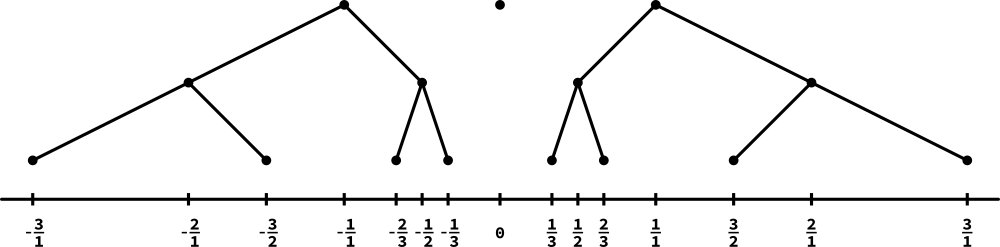
The figure above shows the first three levels of the signed Stern-Brocot tree SSB. Each path in in the right binary tree represents a positive rational number while each in the left a negative rational number. Irrational numbers can be represented as infinite lazy sequences on the trees [3].
The SSB is related to representation of numbers as continued fractions and in 1972 Bill Gosper found an algorithm for arithmetics on continued fractions [1]. In 2007, Milad Niqui published a work that generalizes Bill Gospers algorithm onto sequences of SSB [3]. The Clojure implementation here, with some exceptions, closely resembles Milad Niqui's work.
Assuming, you have installed boot, run
boot pom jar install
inside the repository. stern-brocot-tree should then be installed into
your local Maven and can be included into project dependencies.
[stern-brocot-tree "0.0.1"]
Inside a project, reuquire the following functions.
> (require '(stern-brocot [tree :refer [Q->SSB SSB->Q R L fmt]]))
> (require '(stern-brocot [arithmetic :refer [add sub mul div]]))
Q->SSB converts a rational number to its SSB representation and
SSB->Q is its inverse. fmt prints a human readble representation of
the sequence.
> (Q->SSB -2/3)
(-1 #function[stern-brocot.tree/L] #function[stern-brocot.tree/R])
> (fmt *1)
-LR
> (SSB->Q [-1 L R])
-2/3
Irrational numbers are infinite sequences of SSB. For example, √2
can be represented through (1 ~R ~@(cycle [L L R R])). That means we
start in the positive tree and descend right, and then continue
infinitely descending left, left, right, right. The further we we climb
down the tree, the more precise our value of the root.
> (let [s `(1 ~R ~@(cycle [L L R R]))]
(doseq [n (concat (range 2 10) (range 10 46 4))]
(println (format "%-41s %-17s %s"
(fmt (take n s))
(SSB->Q (take n s))
(double (SSB->Q (take n s)))))))
Stern-Brocot sequence Rational Decimal
-----------------------------------------------------------------------------
R 2 2.0
RL 3/2 1.5
RLL 4/3 1.333333333333333
RLLR 7/5 1.4
RLLRR 10/7 1.428571428571429
RLLRRL 17/12 1.416666666666667
RLLRRLL 24/17 1.411764705882353
RLLRRLLR 41/29 1.413793103448276
RLLRRLLRR 58/41 1.414634146341463
RLLRRLLRRLLRR 338/239 1.414225941422594
RLLRRLLRRLLRRLLRR 1970/1393 1.414213926776741
RLLRRLLRRLLRRLLRRLLRR 11482/8119 1.414213573100135
RLLRRLLRRLLRRLLRRLLRRLLRR 66922/47321 1.41421356268887
RLLRRLLRRLLRRLLRRLLRRLLRRLLRR 390050/275807 1.414213562382391
RLLRRLLRRLLRRLLRRLLRRLLRRLLRRLLRR 2273378/1607521 1.414213562373369
RLLRRLLRRLLRRLLRRLLRRLLRRLLRRLLRRLLRR 13250218/9369319 1.414213562373103
RLLRRLLRRLLRRLLRRLLRRLLRRLLRRLLRRLLRRLLRR 77227930/54608393 1.414213562373095
The last decimal, 1.414213562373095, correctly represents the first 16 decimal digits of √2.
The arithmetic operations are add, sub, mul and div and behave
like the ordinary arithmetic operations. The example shows how to add
one to √2.
> (->> (add [1] `(1 ~R ~@(cycle [L L R R])))
(take 42)
SSB->Q
double)
2.414213562373095
- R.W. Gosper (1978), Continued fraction arithmetic, Unpublished draft paper, text available at http://www.tweedledum.com/rwg/cfup.htm (cited Dec 15 2016)
- A. Ya. Khinchin, Continued Fractions, Dover Publications, Mineoa, NY (1961)
- M. Niqui (2007). Exact arithmetic on the Stern–Brocot tree. Journal of Discrete Algorithms, 5(2), 356-379. doi:10.1016/j.jda.2005.03.007
- M. Niqui, Y. Bertot, QArith - A rational arithmetic library for Coq, https://github.com/coq-contribs/qarith-stern-brocot (cited Dec 15 2016)
- R.E. Graham, D.E. Knuth, O. Patashnik, Concrete Mathematics. A Foundation for Computer Science 2nd edition, Addison-Wesley, Reading, MA (1994)