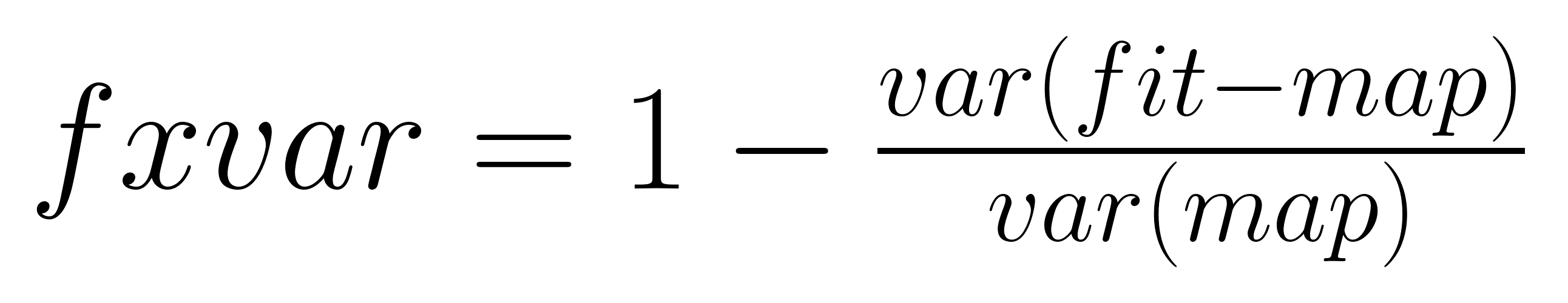Gaussian 2D Fitting

This repository contains code to fit a 2D Gaussian model to given data. A requirements.txt file is provided to install these dependencies. All the code you need is in the gaussian_2d_fitting.py file.

Gaussian 2D Fitting

Simply move the gaussian_2d_fitting.py file to the directory where you want to run the code. Then, import the fit_2d_gaussian function from the gaussian_2d_fitting module.

from gaussian_2d_fitting import fit_2d_gaussian

param_estimate, param_sem = fit_2d_gaussian(numpy_2d_array, plot=True, show=True)

The plot and show arguments are optional. If plot is True, the function will plot the original image and the fitted Gaussian. If show is True, the function will show the plot. The param_estimate and param_sem, stand for parameter estimate and standard error of the estimate, respectively. They are both NamedTuples with the following fields:

class GaussianParameters(NamedTuple):
    amplitude: float
    mu_x: float
    mu_y: float
    sigma_1: float
    sigma_2: float
    theta: float
    offset: float

Simply use the dot notation to access the parameters, e.g., param_estimate.amplitude.

Calculate the Fraction of Explained Variance

The calc_f_explained_var(sum_map: np.ndarray, params: GaussianParameters) -> float function calculates the fraction of explained variance of the fitted Gaussian model.

fxvar = calc_f_explained_var(numpy_2d_array, param_estimate)

The formula for the fraction of explained variance is:

Here:

• fit is the image reconstructed with fit parameters.
• map is the original image.
• var(•) denotes the variance of the given expression.

Examples

Look at the examples.py file for examples of:

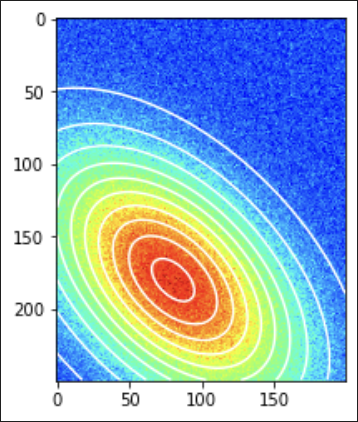
1. Fitting a 2D Gaussian to a single Gaussian.

Explained Variance: 0.95

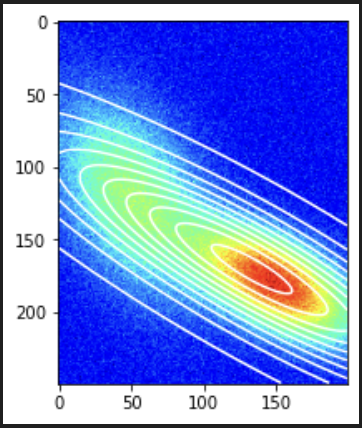
2. Fitting a 2D Gaussian to a sum of two Gaussians.

Explained Variance for Combined Data: 0.85 (Lower because it can only fit one Gaussian)

3. Using multiprocessing to fit multiple images and save the fit in a multipage PDF file.

• A PDF file (./results/fit_results.pdf) containing the plots of the fitted Gaussians.
• A text file (./results/fit_results.txt) containing the estimated parameters, standard errors, and explained variances for each fit.