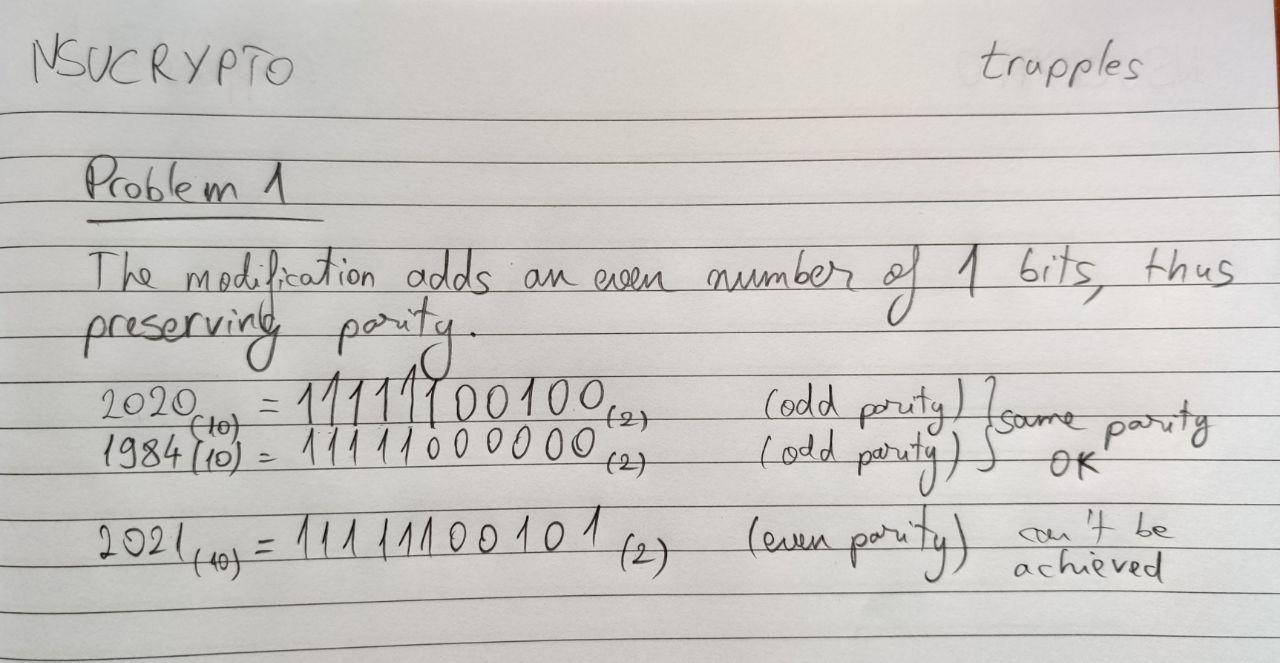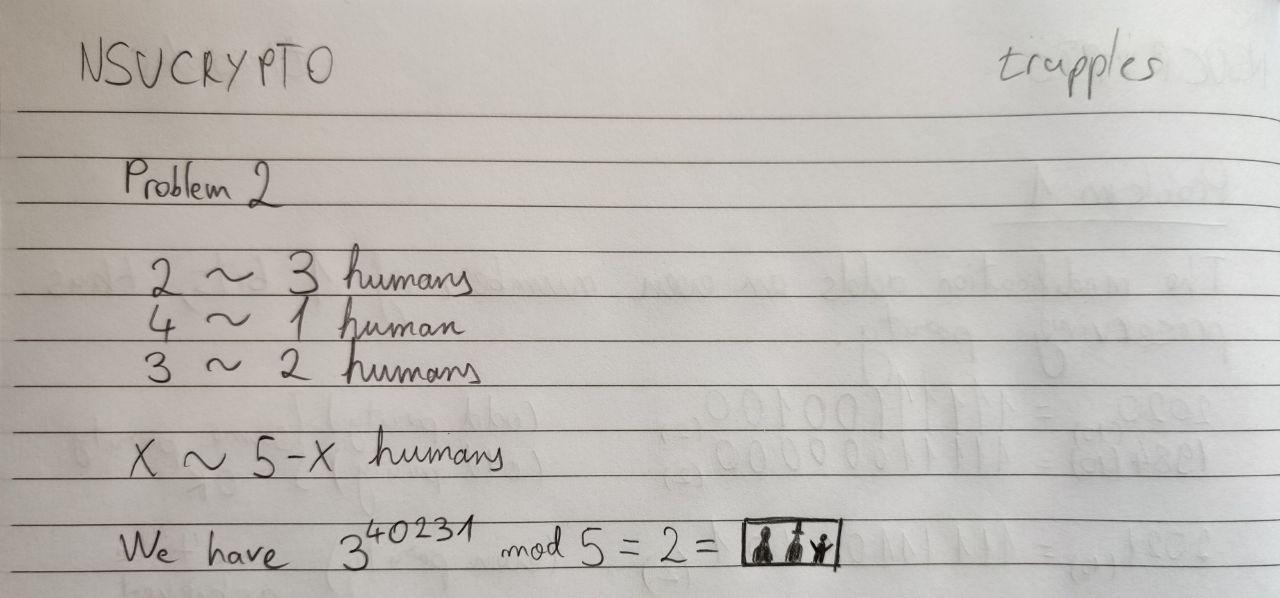| Problem | №1 | №2 | №3 | №4 | №5 | №6 | №7 | Sum |
|---|---|---|---|---|---|---|---|---|
| Max score | 4 | 4 | * | 4 | 4 | 6 | 4 | |
| My score | 4 | 4 | - | 4 | 4 | 6 | 2 | 24 |
No solution.
I initially tried solving it algebraically by considering each query as a matrix multiplication mod 324:
R = ( 1 18 )
( 18 -1 )
G = ( 17 6 )
( -6 17 )
B = ( -10 -15 )
( 15 -10 )
With the goal of getting from (20,20) to (0,0) mod 324.
A very nice property was that B*G = G*B, so they commute, so you can rearrange any sequence of consecutive B and G queries to something like B^b * G^g, b,g natural numbers.
Unfortunately, R does not have this property. If it had had it, it would have been possible to rearrange the entire sequence of moves to this form:
R^r * G^g * B^b * (20,20) , with r,g,b natural numbers
Oh well, i was probably on the right track, but I figured I could just make a directed graph which describes how each element in Z_324^2 can be transformed by the 3 matrices, and then show there is no path from (20,20) to (0,0).
I am not storing the graph structure, as from each (a,b) node we can easily compute its 3 direct successors. I am using a basic BFS to get a set of all possible (a,b) values.
Solution script: ./round1/nsu-p4.py
Solution PDF: ./round1/nsu-p5.pdf
This is a classic LSB steganography problem. PNG's lossless compression allows us to encode information by subtly changing the image colors (in this case, using the least significant bit to bear our data), and we know that change will persist, unlike in a lossy compression format like JPEG.
The first tool I try on lossless stegano problems is the infamous stegsolve.jar.
IMAGE MISSING, SEE PDF
I immediately go to bit plane 0 of each color channel and noticethe telltale signs of LSB stegano: it is almost full with zeros (whereas an actual image would have a random distribution of 0 and 1), except for the very beginning, the first row:
IMAGE MISSING, SEE PDF
Stegsolve has an integrated tool for LSB extraction in Analyse>Data extract, which helps us successfully extract the message:
IMAGE MISSING, SEE PDF
They know that you are a spy! Get back to the center right now.
We now know that Mr. Bob "disappeared" by going to the spy center, whatever that is.
Graders' comment: the number of queries can be reduced
We can solve this with a 100% success rate in 3 queries:
query 1:
- victor sends (z1, z2) (implementation: I send the same valid plaintext twice, z1=z2)
- victor receives next_iv = enc(z1^iv) or enc(z2^iv)
query 2:
- victor sends (next_iv, next_iv)
- victor receives enc(0)
query 3:
- victor sends (enc(0), z3), z3 != enc(0). (implementation: I generate a valid plaintext different to z3)
- victor either receives enc(0) again, case in which b=0, or not, case in which b=1
Solution script: ./round1/nsu-p6.py
Graders's comment: Good effort, but no proof of the correctness of the algorithm.
My round 1 solution script describes an O(N^2) algorithm and further optimises it to O(NlogN). Check out our round 2 solution below for an O(N) algorithm created by @GabiTulba.
TODO
| Problem | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 | №9 | №10 | Sum |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Max score | 4 | 7 | 6 | 12 | * | * | 6 | 8 | * | * | |
| Our score | 4 | - | 6 | 4 | 3 | 6 X | 6 | 8 Y | 3 | 11 | 51 |
X: Open problem - The problem is SOLVED. Y: BEST SOLUTION!
No solution.
trupples: While we (but mostly Gabies) explored the subject, we could not find any significant breakthrough.
Problem 3. Hidden RSA
./round2/writeup-3.pdf ./round2/rsa.py - Requires yafu ./round2/rsa-hardcoded-pq.py - Does not require yafu
trupples: We were mega hyped to see how this did and thought we had an excellent solution, but apparently we pretty much flunked it from the start. Still, it was a very nice exercise in technical writing which we were, at least initially, very very very proud of!
Graders' comment: Q1. Wrong answer. Q2. A partial solution. Note that \theta and \pi are permutations. You get relations such that \pi is a permutation but forget about conditions on \theta. So, you only get a partial solution. Therefore, your total number of solutions (including 36864 ) are wrong because you consider r1,r2,c1,c2,q1,q2,b1,b2 such that \theta is not a permutation.
[./round2/dihedral.py] - The beautiful yet wrong script that led us to wrong suppositions about the structure of orthomorphisms AAAAA
trupples: I loved the idea for this task, and thought I'd do well, so I left it to the last 2 days. Turns out my compression ideas were absolute trash and barely managed to improve the initial compression ratio by a couple percent.
Graders' comment: The authors provide discussion how they improve the compression but they do not provide any code confirming their proposed algorithm at all. Some of their ideas look correct but we can not confirm their numbers because the code is absent.
trupples: oops
./round2/nsu-p5.py - Horribly messy script that benchmarks a handful of compression schemes
Graders' comment: Q1 OK! Q2 Solved. Although not entirely accurate reasoning. But one can catch the right answer. Interesting handling of Carmichael numbers.
TODO @GabiTulba
Graders' comment: OK! (Note: the number of queries can be reduced).
./round2/nsu-p7.py - Basically the same script as round 1. Turns out you can do it in less queries!
Graders' comment: Correct solution for all 3 subproblems. Great presentation!
trupples: I mega half assed this, and didn't even correctly interpret the task at hand 🤦 Better luck next time.
Graders' comment: No mathematical solution proposed by these authors, only a program that looks correct but is very basic. No result of the program is given. Note. The rating scale has been slightly revised.
./round2/bases.py - Exploration attempts..
TODO @GabiTulba