Calculation of the dynamic balance of reciprocating and rotating masses of internal combustion engines
engine_balance.py is designed to calculate the dynamic balance of reciprocating and rotating masses of internal combustion engines.
This tool is a Python revision of a program created in 1978 for a graduation project at the Belarusian National Technical University. The original program was written in "ap" ("ап") language for computer "NAIRI-2".
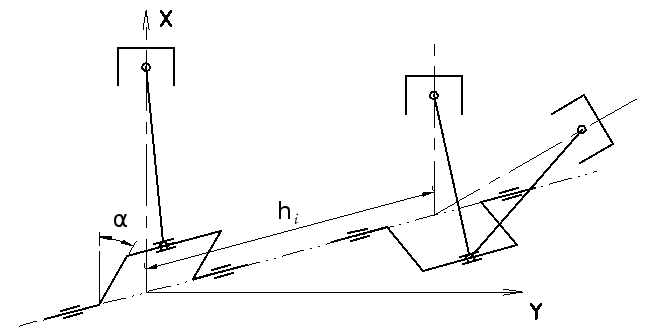
Fig. 1
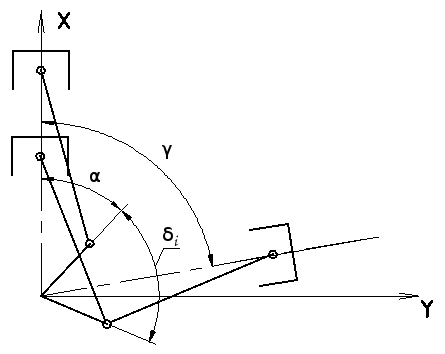
Fig. 2
The following abbreviations are used:
-
Železko B.E. Osnovy teorii i dinamika avtomobilnych i traktornych dvigatelej. Minsk : Vysšaja škola, 1980 / Железко Б.Е. Основы теории и динамика автомобильных и тракторных двигателей. Мн. : Выш. школа, 1980.
-
Alberto Dagna , Cristiana Delprete, Chiara Gastaldi. A General Framework for Crankshaft Balancing and Counterweight Design. Department of Mechanical and Aerospace Engineering, Politecnico di Torino. Appl. Sci. 2021, 11(19), 8997; https://doi.org/10.3390/app11198997.