MATLAB code for the paper, Deep coregionalization (DC) for the emulation of simulation-based spatial-temporal fields (https://www.sciencedirect.com/science/article/pii/S0021999120307580).
Essentially, the method is a combination of residual principal component analysis (rPCA) and Nonlinear autoregression (NAR) for multi-fidelity spatial-temporal field emulations.
Please refer Demo_dc.m for the usage of the code. Please add all subfolder to your matlab path to start using the code.
The following are figures are taken from the paper.
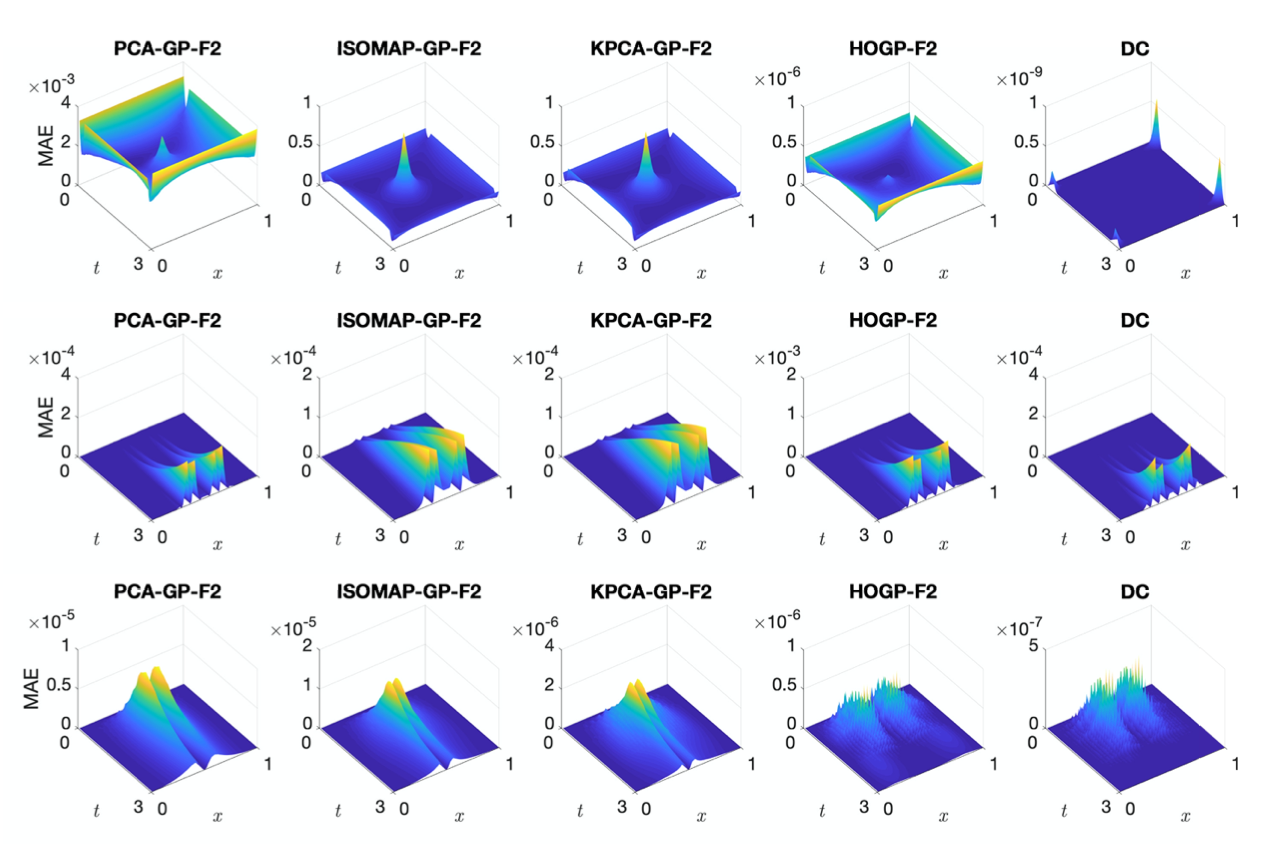 MAE field for Poisson’s equation (top row), heat equation (middle row) and Burger’s equation (bottom row). Deep coregionalization uses 256 Fidelity-1 and 32 Fidelity-2 samples, whereas the other methods use 256 Fidelity-2 samples; the low rank is fixed at R = 8. The error fields show similar patterns for the same PDE. The superiority of deep coregionalization is clearly revealed by its error scale with 8 times fewer Fidelity-2 samples.
MAE field for Poisson’s equation (top row), heat equation (middle row) and Burger’s equation (bottom row). Deep coregionalization uses 256 Fidelity-1 and 32 Fidelity-2 samples, whereas the other methods use 256 Fidelity-2 samples; the low rank is fixed at R = 8. The error fields show similar patterns for the same PDE. The superiority of deep coregionalization is clearly revealed by its error scale with 8 times fewer Fidelity-2 samples.
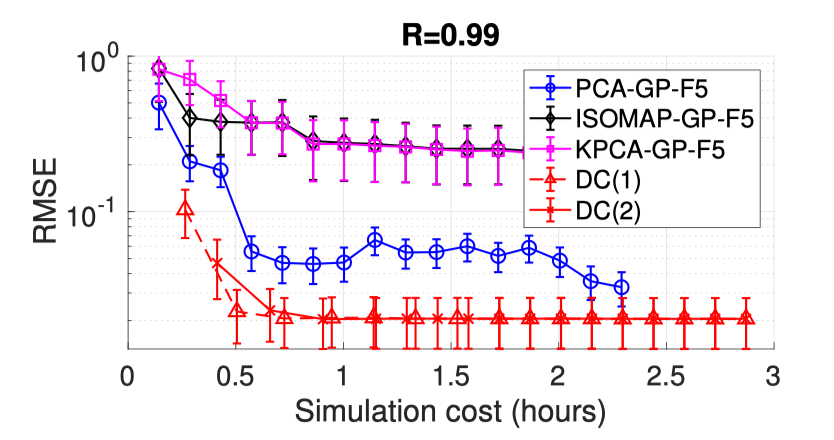 RMSE as a function of the computational cost of generating the training data for the Navier-Stokes (NS) spatial-temporal simulation.
RMSE as a function of the computational cost of generating the training data for the Navier-Stokes (NS) spatial-temporal simulation.
Please cite the paper if you find this code useful.
@article{XING2021109984, title = {Deep coregionalization for the emulation of simulation-based spatial-temporal fields}, journal = {Journal of Computational Physics}, volume = {428}, pages = {109984}, year = {2021}, issn = {0021-9991}, doi = {https://doi.org/10.1016/j.jcp.2020.109984}, url = {https://www.sciencedirect.com/science/article/pii/S0021999120307580}, author = {Wei W. Xing and Robert M. Kirby and Shandian Zhe}, keywords = {Surrogate model, Gaussian process, Emulation, Spatial-temporal field, Multifidelity model}}