阿涛在努力,前端说白了就是Javascript,不要怂,就是刚,Javascript语言的数据结构和算法 从现在开始!
1.1) 冒泡排序: 复杂度为O(n^2),简单地说下思路就是用for循环比较 前者比后者大 换下位置。
1.2) 选择排序: 复杂度为O(n^2),原址比较排序算法,找到数构最小值放第一,第二小放第二,就是这样。
总结: 这两个活宝排序算法还是比较像的,一个冒泡越往右泡越大,一个往左先确定最小的,再第二小。
1.3) 插入排序: 复杂度为O(n^2),算法是从第二个位置开始的,与前面的比较,比它小的插入前面,这个有点抽象,举个例子 假定arr1的数组为[3,,5,1,4,2],首先我们知道3已经默认排好了,然后我们3和5比,顺序对的就不动,然后1和5比,插上去,再和3比插上去,目前应该是1,3,5. 然后4跟5比插上去,跟3比不插,现在是1,3,4,5,然后2跟5比插上去跟4比插上去3比插上去跟1比不用插,至此1,2,3,4,5 排序完成。
1.4)归并排序:thumbsup:: 复杂度为O(nlog^n),相比前三个这个要好很多啊,它其实是一种分支算法,把一个原始数组劈开拆分成较小数组进行比较,将结果插入到新的结果集数组 中去,由于是分治算法,所有它是递归的。我还是举个例子吧,比如[3,4,1,2]这个数组,一刀劈开分成[3,4]和[1,2]这两个,然后3和1比把1插入结果集[1],继续比4和2把2插入 结果集[1,2],然后比完这一趟,把[3,4]劈开,进行比较,[1,2,3,4]出来了走你!
1.5)基数排序: 这个是在学队列的时候,比方说用一个随机数构造两位数10个,然后呢 ,按个位数一次进出队列,按十位数一次进出队列,然后答案很明了了。
对于数组的定义一般是一个存储元素的线性集合,但是Javascript数组6啊,我们不一样, 它准确的来说是一种对象(Object),偏移量的索引代表它的属性,数字索引在内部会被转换为 字符串,因此JavaScript对象的属性名必须是字符串,因为人家是个对象,所有效率比其他语言差点
简单粗暴的创建数组方式
var arr=[]; //数组length=0
稍微温柔点
var arr=[1,9,9,7,0,6,1,3] //长度是8,数字是我的生日
搞对象方式创建
var arr=new Array(); //对象嘛,没啥好解释的
温柔地搞对象创建
var arr=new Array(1,9,9,7,0,6,1,3) //构造函数传参
Javascript作为脚本之王,有一点很秀的是,它这个数组里的值不一定是同类型的
关于数组对象的属性
length:长度(JS中数组的长度可以任意增长,秀不秀,length只是当前长度,用于遍历数组)
关于数组的方法
isArray(arr):判断是不是数组
push()/unshift():添加元素(可变函数),push()在最后添加,unshift()在最前面添加
pop()/shift():从数组末尾删除元素/从数组开头删
(last)indexOf():查传进来的参数在目标中是否存在(存取函数),正确返回索引,错误-1 index是第一个,带last的是最后一个,就是一个从左往右读,一个从右往左读,但是索引都是从左往右的
join()/toString():转成字符串,join()括号可带东西功能略强大
reverse()/sort()(可变函数):前者是将元素的顺序翻转,后者则是字典排序并非按大小的,比方说你可以试下1 100 2 3 4,结果100并不是最后,这里改进它用大小比较的方法是传入一个比较函数把它作为参数,让它不按字典排序
那些转数组的方法
String转数组:split() //框号里面可以写分隔符
arr1.concat(arr2):合并多个数组到一个数组
arr.splice(index,length):截取数组某个子集到一个数组,起始索引(从0开始,从索引处开始删),长度,截取后源数组被截取的就没了啊,如果长度为0,然后你再添加个参数就是插入元素了,这个也是可变函数
关于数组赋值给其他数组
浅复制
给赋值的数组增加引用,但修改引用数组,赋值数组会一起变化
深复制
给赋值的数组增加引用,但修改引用数组,赋值数组不会变化
可变函数: JavaScript中可以不必引用数组中的某个元素,就能改变数组的内容的函数
不生成新数组的迭代器方法: foreach()、every()、some()、reduce()和reduceRight()函数 ,其中foreach()接收一个函数作为参数,every和some接收一个返回值为Boolean类型的函数,前者所有的为true才是true,后者只要满足一个true就是true reduce()函数的话用于累加值计算,如果是数字返回累加结果,如果是字符串返回 字符串句子,reduceRight()就是从右边开始
生成新数组的迭代器方法: filter()和map(),map()和foreach()类似但是会产生新数组,filter()和every()类似,但是所有为true就会产生一个新数组,这个真的很有用
二位数组: Javascript只支持一维数组,但是我们可以嵌套进去一维数组,这样就形成了二维数组
二维数组操作: 这里我们知道二维应该时一个平面,那么它就有两条基准线,x和y分别对应横纵坐标,一组嵌入式的for循环,如果时按列访问,那么最外面一层时行,最里面时列,反正亦然, 说到这个二维,有的时候哪有凑的那么好方方正正,可能每个维度的长度不一样,但是你会发现Javascript处理起来的效果还是令人满意的
对象数组: 就是数组里有对象哇,我们知道创建对象可以有工厂方法,构造函数传参,原型链等,昨天晚上很晚了用构造函数传参发现一直是undefined,真让人头大,分析 了下思路又是对的,真的是不解,今天在构造函数里写了两个获取x和y的方法,让人头大的是又来了,答案是很明朗了,可是为什么会有第三个参数NaN就有点迷,最后脑子还是多转了一圈 为什么它获取的是undefined,也就是它拿不到创建的对象的参数的值喽,真相就是----答案只有一个 没用返回this指针,最后终于解决了这个问题,开心!
定义:一组有序数据,在Javascript中列表数据类型可不相同,在Javascript中列表数据类型可不相同,在Javascript中列表数据类型可不相同, 重要的事情说三遍,元素个数没有限定,但内存是有限的,应用场景是数据结构不复杂然后数据量不大,那,就是它啦。
列表的抽象数据类型(ADT)定义如下:
| 属性和方法 | 含义解释 |
|---|---|
| listSize | 列表的元素个数 |
| pos | 列表的当前位置 |
| length() | 返回列表中元素个数 |
| clear() | 清空列表中所有元素 |
| toString() | 返回列表的字符串形式 |
| getElement() | 返回当前位置的元素 |
| insert() | 在现有元素后插入新元素 |
| append() | 在列表的末尾插入新元素 |
| remove() | 从列表中删除元素 |
| front() | 将列表的当前位置移动到第一个元素 |
| end() | 将列表的当前位置移动到最后一个元素 |
| pre() | 将当前位置前移一位 |
| next() | 将当前位置后移一位 |
| currPos() | 返回列表的当前位置 |
| moveTo(n) | 将当前位置移动到指定位置 |
注意: 在使用迭代器遍历,由于数组的长度是可变的,所有会进入一个死循环请加点判断让他停下来
for(list.front();list.currPos()<list.length();list.next()){
console.log(list.getElement());
} //这种写法根本 停不下来好嘛 1 2 2 2 2 2 2 .........
定义:这个我们这样子啊,书上是洗盘子的例子,确实挺生动形象的,有个更生动形象的是 浙工大就业的孙老师那个,什么时候投递简历最合适,当然是早上八九点,因为hr小姐姐刚上班 根据堆栈原理,一打开邮箱可不是你的嘛,大兄弟!
栈的主要属性和函数说明
| 属性和方法 | 说明 |
|---|---|
| top | 栈顶 |
| bottom | 栈底 |
| push() | 进栈 |
| pop() | 出栈 |
| pee() | 返回栈顶元素但不删除 |
栈的运用: 进制转换、判断字符串是否回文,递归运算
定义:先进来的先出去,食堂买饭排队(当然插队的不法分子没教养没素质的 不算)就是队列
队列的主要属性和函数说明
| 属性和方法 | 说明 |
|---|---|
| front() | 队头 |
| back() | 队尾 |
| enqueue() | 入队 |
| dequeue() | 出队 |
| peek() | 读取队头 |
队列的运用: 基数排序、优先队列(不遵守FIFO的)
定义:链表是一组节点组成的集合。每个节点都使用一个对象的引用指向它的后继,指向另一个节点的引用叫做链,。这个是书上说的, 接地气点讲就是那种链子,一条一条的哇。下面来造条链子 Header=>A=>B=>C=>D=>null。就这个意思啦。
链表的构造
| 类 | 说明 |
|---|---|
| Node | 表示节点 |
| LinkedList | 提供一些方法 |
节点节点 一层一层 地拨开我的心
LinkedList {
head:
Node {
element: 'head',
next: Node { element: 'Hangzhou', next: [Node] } },
find: [Function: find],
insert: [Function: insert],
display: [Function: display] }
双向链表: 接楼上的普通链表之后,什么是双向链表呢,楼上那位不是有个next吗,楼下 这位就是比它多了个pre哇,让我联想到了那个冒泡排序,它不是只冒一边的泡吗,这个就是两边都冒喽, 有点这个意思,我们还是直接上例子吧 两条啊, header=>A=>B=>c>null; C=>B=>A=>header=>null
DoubleLinkedList {
head:
Node {
element: 'head',
prev: null,
next: Node { element: 'Hangzhou', prev: [Circular], next: [Node] } },
find: [Function: find],
insert: [Function: insert],
findLast: [Function: findLast],
remove: [Function: remove],
display: [Function: display],
dispReverse: [Function: dispReverse] }
循环链表: 在创建的时候头节点的next指向头节点,说白了就是个圈哇
定义:Dictionary类的基础是Array类,而不是Object类,一种以键值对存储的数据结构,让我想到了JSON,嘿嘿!
Dictionary {
dataStore: [ name: 'ataola', sex: '男', age: '21' ],
add: [Function: add],
find: [Function: find],
remove: [Function: remove],
showAll: [Function: showAll] }
定义:传说中的散列表,基于数组(长度质数为好,除留余数法)设计,所有元素通过该元素对应的键存储,通过散列函数映射。插入删除和取用数据效率高,但查找 它不行的,例如查找最大最小值,稍微虚了点。
基本散列函数: 把每位选手的ascii值相加与数组的长度进行取余运算(这种情况要是遇到散列值一样的,后面的就会覆盖前面的,对否)
function simpleHash(data) {
var total = 0;
for (var i = 0; i < data.length; i++) {
total += data.charCodeAt(i);
}
console.log("Hash value: " + data + "->" + total);
return total % this.table.length;
}
Hash value: A->65
Hash value: C->67
Hash value: B->66
Hash value: b->98
Hash value: a->97
Hash value: c->99
Hash value: ab->195
Hash value: AB->131
Hash value: ad->197
Hash value: da->197
霍纳算法: 在楼上那位的基础上,每次求和乘以一个质数,当然啦,质数怎么选也是有技巧的,比较JavaScript是处理I/O密集的选手而不是计算
function betterHash(data) {
var N=37;
var total=0;
for(var i=0;i<data.length;i++){
total=total*N+data.charCodeAt(i);
}
console.log("Hash value: " + data + "->" + total);
return total%this.table.length;
}
Hash value: A->65
Hash value: C->67
Hash value: B->66
Hash value: b->98
Hash value: a->97
Hash value: c->99
Hash value: ab->3687
Hash value: AB->2471
Hash value: ad->3689
Hash value: da->3797
应用: 学生的ID和成绩散列
解决碰撞: 开链法和线性探测法
开链法:也就是创建了一个二维数组
function buildChains(){
for(var i=0;i<this.table.length;i++){
this.table[i]=new Array();
}
}
线性探测法:在hashtable类中添加一个数组属性,然后分别在get、put里面分开放
定义:一种包含不同元素的数据结构,元素称之为成员,和高中数学讲得一样,具有互斥性和无序性,关于一些集合的概念扔给数学吧, 但 空集 子集 交集 并集 补集 要心里有个数
定义:树么,就是有根茎叶花果实种子那货,讲得生物了一点,就那个意思。有根节点(第0层)、子节点、有叶子节层,层数即树的深度,访问树种所有节点称为树的遍历, 每个节点有关的值称之为 键
二叉树: 二叉树是一种特殊的树,子节点不查过两个,左节点较小,右节点较大,这是棵规律树啊,所以查找效率高
二叉查找树(BST): 这个其实相比前面的数据结构可以说是有点复杂了,具体的是体现在用编程语言的实现
insert()函数如下:一定要好好理解,不理解的话一段时间后就会忘了哦
function insert(data) {
//插入元素节点化
var n=new Node(data,null,null);
//如果根节点是null的话,设根节点为当前插入节点
if(this.root==null){
this.root=n;
}
else{
//把根节点赋值给当前节点
var current=this.root;
//父节点
var parent;
while (true){
//把当前节点赋值给父节点
parent=current;
//如果插入的节点数据小于当前节点数据的话,设新的当前节点为原节点的左节点
if(data<current.data){
current=current.left;
//如果当前节点的左节点为null,那么新节点插入这个位置,退出循环
if(current==null){
parent.left=n;
break;
}
}else {
//否则,设当前节点为原节点的右节点
current=current.right;
//如果当前节点的右节点为null,呢么新节点插入这个位置,退出循环
if(current==null){
parent.right=n;
break;
}
}
}
}
}
在有了插入后,我们肯定是想遍历它得到结果,遍历的话,我们这样思考,一个不正常树,比方说它是一个三角形的深度为2的东东(自行脑补),要么从左节点,要么右节点 要么中间那个,所以咯,先序(不是前序,别问我为什么,规矩啊)、中序、后序哇。
总结下遍历吧:
先序:根=>左=>右
中序:左=>根=>右(按节点键值升序递归访问)
function inOrder(node) {
if(!(node==null)){
inOrder(node.left);
console.log(node.show()+" ");
inOrder(node.right);
}
}
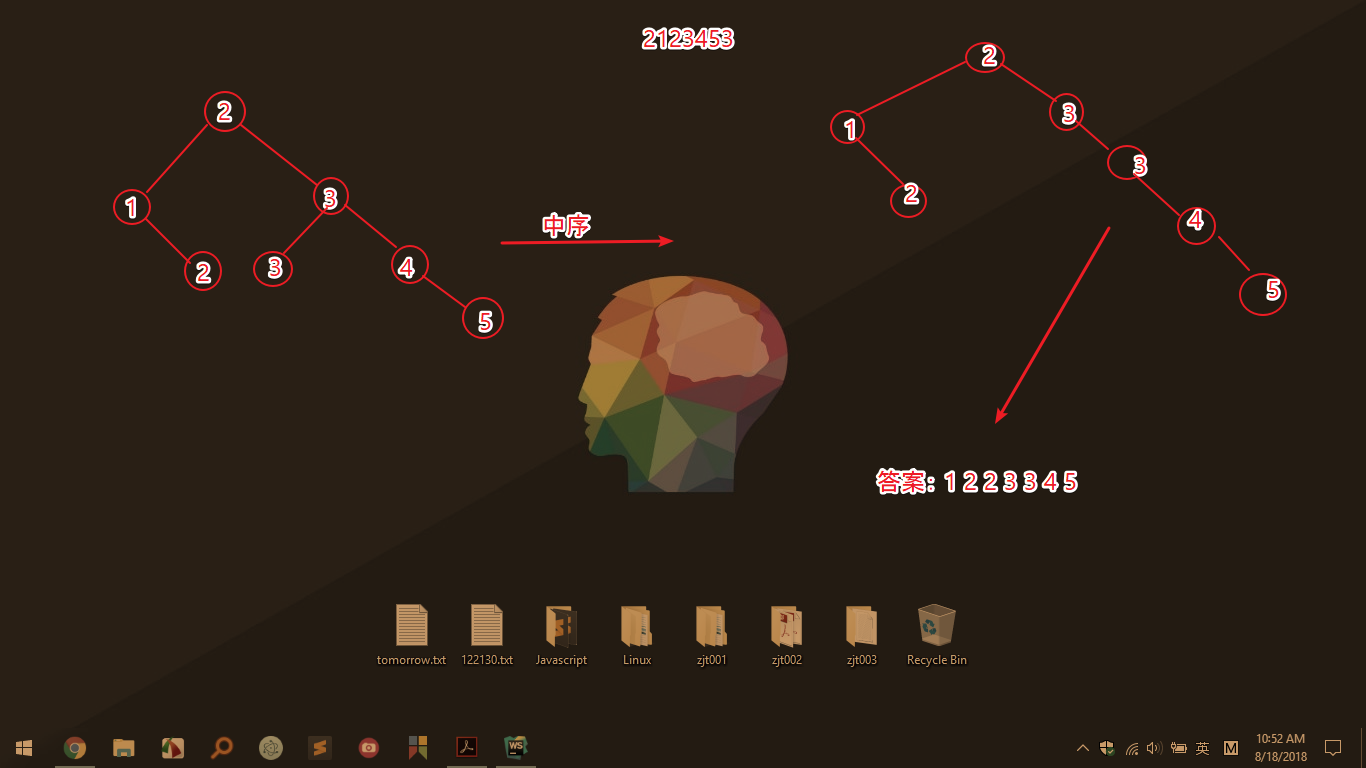
昨天弄得很晚了,挖了个坑让自己跳进去,然后提交的时候脑子一热,忘记之前提交的散列和集合没有push,和二叉树一起push了尴尬。 昨天我在想构造树的时候随便乱想,就想了个 1 2 2 3 3 4 5这种,然后把它拆乱了插入,有没有发现一个问题,就是有很多是一样的值,那它会怎么走, 因为在插入的时候我没有判断等于的情况,然后要确定一棵树至少要两种遍历,看下图脑补的,默认相等放左边的结果:
后序:左=>右=>根
最后还是把先序、中序、后序输出了一遍,发现自己之前的想法是错的,不得不说自己的脑洞真大 哈哈哈哈
// bst.inOrder(bst.root); //1 2 2 3 3 4 5 管你怎么插入它的答案是不变的
// bst.preOrder(bst.root); // 2 1 2 3 4 3 5
// bst.nextOrder(bst.root); // 1 3 5 4 3 2 2
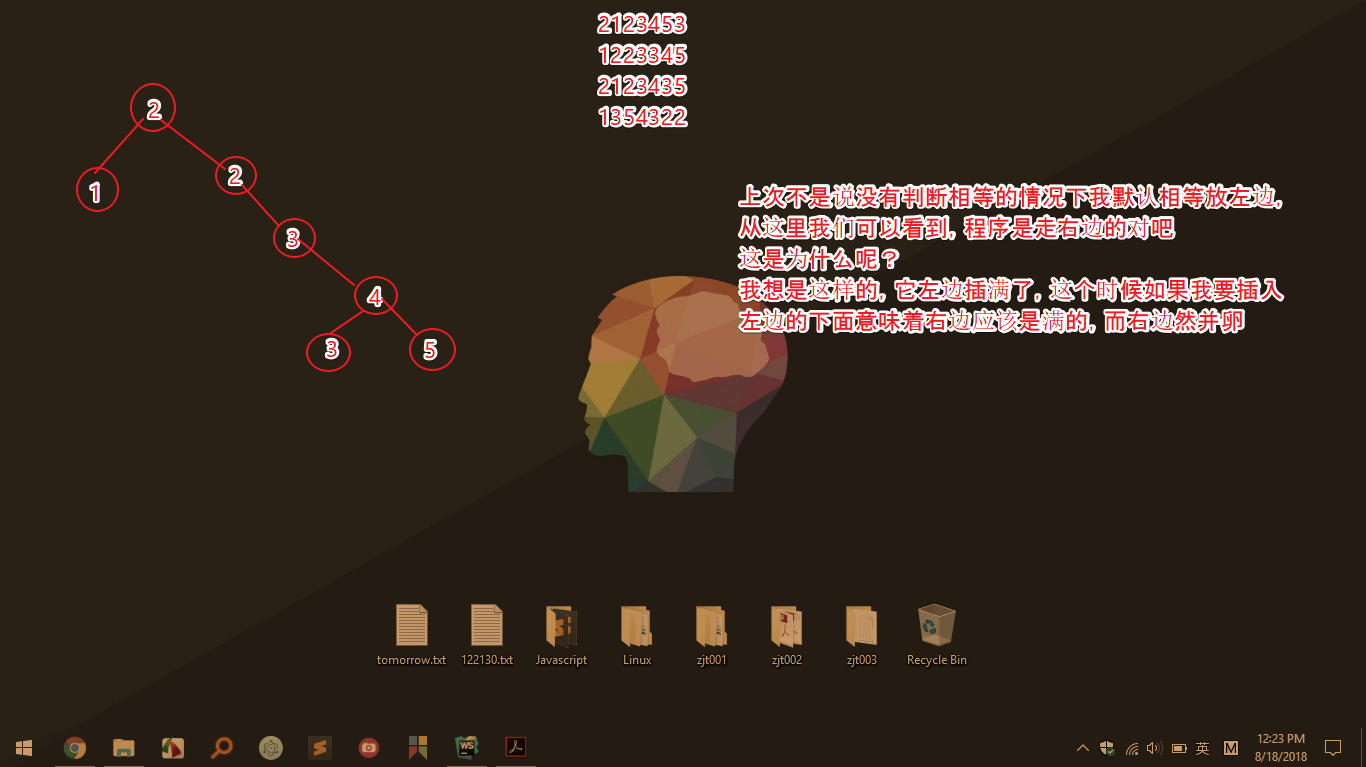
如下是正确的树,不过就是因为有了这个经历,印象深刻了许多
总结我犯得错误是焦点还是在父节点上而不是子节点,这里后序遍历可以确定根节点的位置是最后一个,中序遍历的话是中间那个。
查找二叉树的值: 最大值(遍历右子树到底)、最小值(遍历左子树到底)、指定值(如果小于左节点找,大于右节点找,等于的话返回)
BST删除节点(较为复杂): 如果要删除的节点没有子节点 那 还好, 如果有一个还凑合,如果有两个,真让人头大
用途: 记录一组数据集中数据出现次数
定义:图是由边的集合和定点的集合组成。如果一个图的顶点对是有序的,则称之为有向图,简单地说就是有箭头的,没有箭头的就是无序图。 在无序图中,由指向自身的定点组成的路径称为环,环的长度为0。圈就是至少有一条边的路径,且路径的第一个定点和最后一个相同,如果两个定点有路径, 那么这两个顶点就是强联通,有向图想要强连通那必须是所有的定点都是强联通。
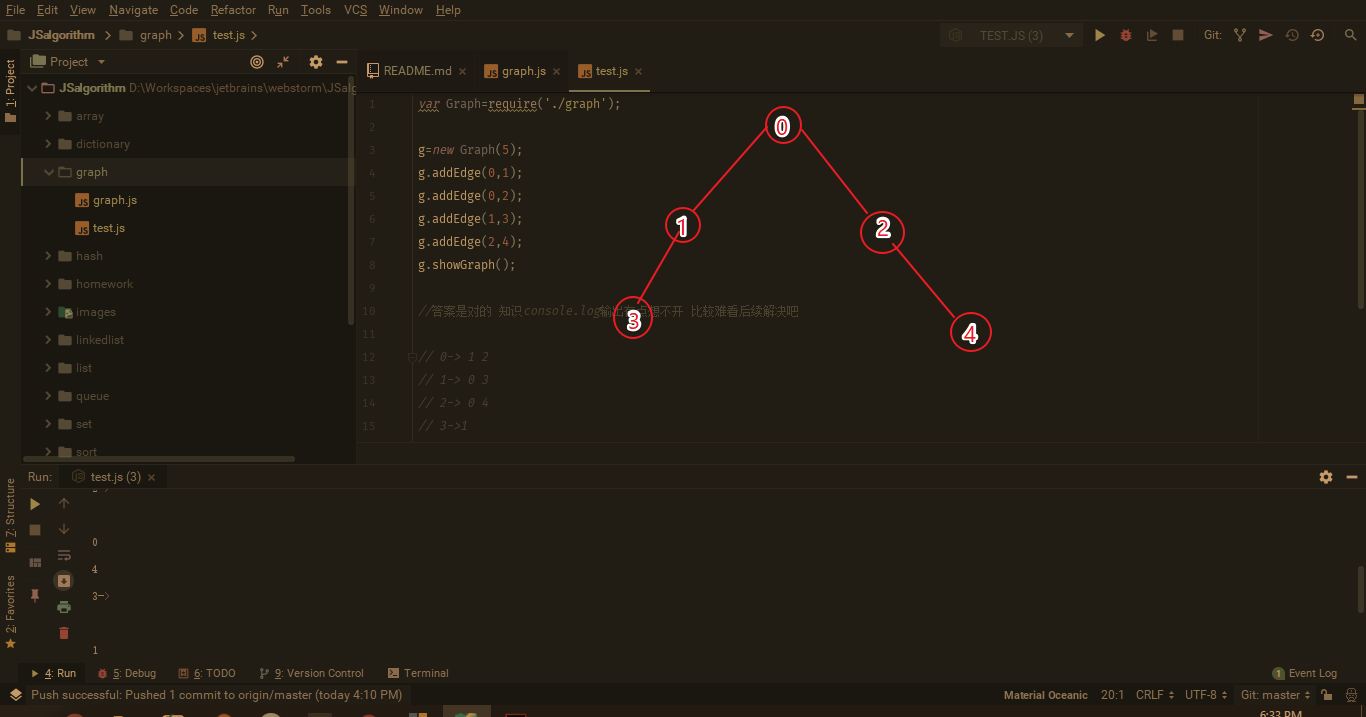
图类:
顶点表示:就是表示顶点哇
边表示:邻接表(邻接矩阵,二维数组)和邻接表数组(就是把顶点搞成一维数组,然后在它后面写上与它相连的顶点)
搜索图:(重点理解下,一段时间感觉会忘)
深度优先搜索:访问一个没有访问过的定点,将它标记为已访问,再递归地去访问在初始定点地邻接表中其他没有访问过的顶点
广度优先搜索:从第一个节点开始,访问经可能靠近它地顶点,广度嘛,横向地。
查找最短路径: 这个很容易想到,那么多线绕来绕去,总有一个是最短的,采用广度优先搜索算法。
拓扑排序: 会对有向图的所有顶点进行排序,使有向边从前面的顶点指向后面的顶点