Mainly 3D printed manipulator with 6 axis of freedom based on design of steward platform
!!! Now the notes in this repository are rather assumptions that will need to be verified in practice !!!
Platform is based on two nearly triangular bases connected with 6 linear actuators.
Control of these actuators is driven from motherboard.
Lower base is stationary, upper base part is movable.
Motherboard is positioned in lower triangle base. Motherboard communicates with controller (pc) via serial line with G-code.
First version of platform is 3D printed. Next version are supposed to be from aluminium.
Motion system is based on affine transformation.
Basic system contains from seven points. Which are placed in center of platform and in points of connection with actuators.
Points are on both triangular bases. Corresponding points have same numbers.
Position of point is described as coordinates in cartesian system.
Center point is not used for calculation of motion, is used only as center point of mass.
- Represent zero-point in three-dimensional space
- Zero point of Z is when platform is set to minimal height (home position)
- Can probably be used for optimization of speed
- Center point can be used to determinate unreachable positions (not all) and as center position of object for affine transformations
Every point is represented as vector [x,y,z,1].
Distance between connect points of actuator on lower and upper bases is calculated.
- Calculation is based on usage of euclidian distance calculation in three dimensional space
$d(a,b) = \sqrt{(a_x - b_x)^2 + (a_y - b_y)^2 + (a_z - b_z)^2}$
Affine transformation is applied on all point of connection with actuators on upper base.
Now is calculated new distance between fixed and movable points. Difference between distances in old and new position is travel distance of actuator.
By repeating this process for every actuator is calculated one move of platform.
Rotation terms: Pitch(X), Roll(Y), Yaw(Z)
Speed scaling is linear based on travel distance of actuator.
Acceleration must grow proportionally as speed.
Traveled distance is integration of actual speed of motor by time.
Example: Two motor M1 - travels 10mm, M2 - travels 30mm,
- Maximal speed is tested (before usage of device) and used for motor with the longest distance (as well as acceleration)
- M1 use three-times lower speed and acceleration because of travel distance is three-times lower
- Travel time is same for both motor, so motors cannot jam due to incorrect position
Jams of platforms are possible when movement is not synchronized. In this state some motor can be in end-position, but motion is not done.
Main issue is when position of points in unknown. This happens when platform is powered on. Before power of platform must be homed -> this cannot be reliably secured.
Possible homing sequence is that all actuators will be moved with same speed to their home position. But there is possibility of jam.
This example is calculated only for one actuators, others have same calculations.
Platform is now at home position. So position of points describes offset from zero point.
Length of all actuator is same. Probably zero length of pushrods + length of body.
In this example is body length two times retractable length. Minimal length 30mm, maximal length is 50mm.
Length is calculated between mates connecting base and actuator.
Point on upper base ([-2, 0, 0, 1], motions are shift forward (Y+2), and rotation to right(Z+90°).
Point on lower base ([-1, 2, -2.45, 1], Z offset is determinated by vertical distance between lower and upper base in home state.
Shift matrix:
$\begin{bmatrix}1 & 0 & 0 & X \0 & 1 & 0 & Y \ 0 & 0 & 1 & Z \ 0 & 0 & 0 & 1 \\end{bmatrix}$
Rotation matrix around Z - Yaw(
$\begin{bmatrix}\cos(\gamma) & -\sin(\gamma) & 0 & 0 \\sin(\gamma) & \cos(\gamma) & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \\end{bmatrix}$
Multiplication of matrix
Note: if platform is not home is necessary to make another translation of object from current position of center point to center of space. This is represented as empty translation-1 matrix
[Translation-1 * Rotation * Translation * Point]
New coordinates of [-2, -2, 0, 1]
Old distance between
- Calculation:
$d = \sqrt{(-2 - -1)^2 + (0 - 2)^2 + (0 - -2.45)^2} = 3.317$
New distance between
- Calculation:
$d = \sqrt{(-2 - -1)^2 + (-2 - 2)^2 + (0 - -2.45)^2} = 4.796$
Difference between old and new length of actuator is: 1.479 cm
So actuator must change length to 4.796 cm, which is nearly maximal length (in this example).
Change of length is + 1.479 cm, speed and acceleration depends on motion of other actuators.
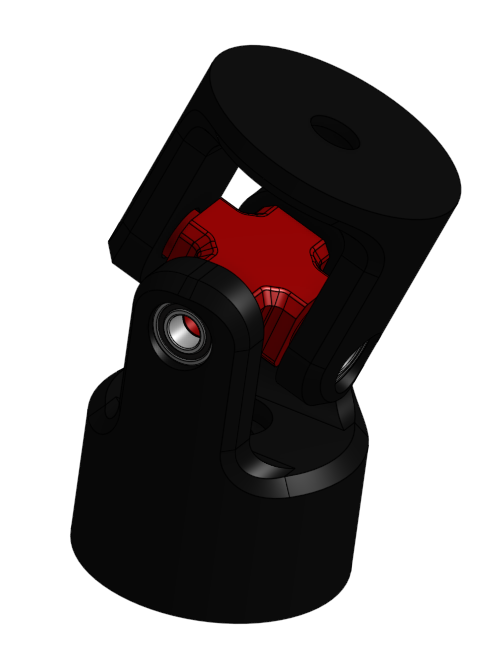
Linear actuators are connected with hexagonal platform with universal joint with can give joint freedom to move freely. Rotation of joint should not be constrained by joint but by length of arm (linear actuator length).
Joints consists of 3 parts. Two forks and one central block. X and Y axis of forks are perpendicular between forks (forks are turned against self by 90° on Z axis). Fork is connected to central block through small ball bearing. This ball bearing removed as much of friction as possible.
Main Motherboard contains six stepper motor drivers L6470 in TSSOP28 package.
PCB is designed with maximal dimensions of 10x7cm, so it can be cheaply manufactured.
- Maximal input voltage is 36V
- PCB is designed for maximal current of 8A into motor, this assumes 6x1.2A stepper motors
- Input stage contains current sensor for monitoring of actual current
- Stepper motor end position can be detected via driver build-in stall detection or through endstop (one per each stepper)
- Endstop should be Normally Open and connect ground to sense pin
- Connector contains 3.3V power output for powering some position sensor instead of tactile switch between sense and ground
- Stepper drivers are in line, so heatsinks can be fit on them
- Via EXT IDC connector can be connected sensor for motion feedback over SPI or I2C
- DEBUG connector pinout is compatible with 10-pin IDC Saleae layout
- Minimal width trace is 5.1 mils (0.13 mm)
- Minimal drill size id 0.3mm